|
physique chimie ( d'après concours 2000) Etude d'un pendule simple |
|||
|
|||
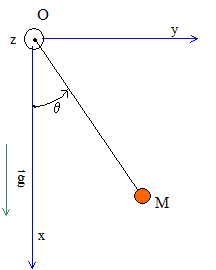
Enoncé du théorème du moment cinétique appliqué à un point matériel : Le référentiel d'étude étant galiléen : La dérivée par rapport au temps du moment
cinétique du point matériel M par rapport au
point fixe O est égal au moment, par rapport à
ce point, de la somme vectorielle des forces agissant sur le
point matériel M . La masse m est soumise à deux forces : la tension du fil et son poids.
(1) : j'exprime le moment cinétique (2) Le moment, par rapport à O, de la tension est nul : cette force rencontre le point O. (3) : j'exprime le moment en O du poids. (4) : j'applique le théorème du moment cinétique (4) montre que la trajectoire du point M est plane, celui de la figure. (4) donne l'équation différentielle vérifiée par l'angle q(t) en fonction du temps : q " + g/l sin q = 0 Dans le cas des faibles amplitudes angulaires, on peut confondre sin q et l'angle q exprimé en radian. D'où : q " + g/l q = 0 Expression de la pulsation w0 du mouvement : w0 = (g/l)½. valeur de g : On mesure pour 20 périodes une durée de 40,12 s. T0 = 40,12 / 20 = 2,006 s Or w0 = 2p/T0 =6,28 / 2,006 = 3,13 rad/s. g=w0 2l = 9,80 m s-2.
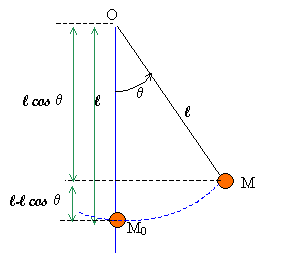
On se place dans le cas d'oscillations d'amplitude plus importante. On désigne par Em l'énergie mécanique, Ep l'énergie potentielle et Ec l'énergie cinétique du pendule. Expressions des énergies cinétique et potentielle en fonction de m, g, l , q et dq/dt = q '. On prend l'origine de l'énergie potentielle pour q = 0. Ec = ½mv2 = ½m(lq ')2.
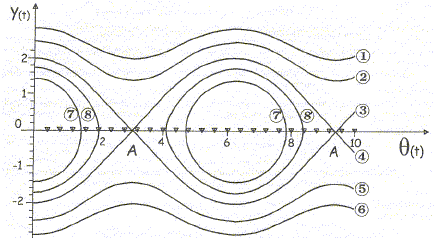
Equation de la trajectoire dans le plan de phase du point P de coordonées q (t) et y = 1/w0dq/dt : Em= ml [½ l q '2 +g (1-cosq)] ; 2Em/( ml )= l q '2 +2g (1-cosq) 2Em/( mg l ) =l /g q '2 +2 (1-cosq) or w0 = (g/l)½ ; 2Em/( mg l ) = (q '/w0 ) 2 +2 (1-cosq) y2 + 2(1-cosq) = 2Em/ (mgl). L'allure générale du portrait de phase de cette équation est donnée ci-dessous :
Les trajectoires de phase 7 et 8 correspondant à
Em<2mgl. Les courbes 1 à 4 correspondent à un mouvement de révolution. |
|||
|
|
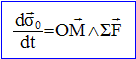

 Ep
= mgl(1-cosq)
Ep
= mgl(1-cosq)