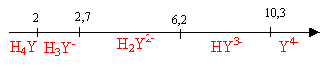|
physique chimie : le Magnésium |
||||||||||||||
|
||||||||||||||
|
Règles permettant d'établir la structure électronique d'un atome polyélectronique : Règle de Pauli : deux électrons se différencient par au moins l'un de leur nombres quantiques n, l, m et s. Règle de Klechkowski : l'ordre de remplissage des orbitales se fait suivant (n+l) croissant ; si deux orbitales atomiques ont le même nombre (l+n), celle qui a la plus faible valeur de n est remplie en premier ( principe de stabilité) 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f... Règle de Hund : cas des orbitales de mêmes énergie. Les électrons de spins parallèles occupent le maximum d'orbitales. Configuration électronique du magnésium dans l'état fondamental :1s2 2s2 2p6 3s2. Forme ionique du magnésium : Mg2+ ; structure électronique 1s2 2s2 2p6 ( couche externe saturée à 8 électrons ) Au cours des réactions chimiques, le magnésium tend à obtenir la structure électronique externe du gaz noble le plus proche. Colonne de la classification périodique se trouve le magnésium : colonne n°2 des alcalino-terreux Chaque élément de cette colonne possède une structure électronique avec deux électrons externes. L'élément précédent le magnésium dans cette colonne est le bérylium de n° atomique 12-8 = 4 ; le suivant est le calcium de n° atomique 12+8 = 20. Energie de première ionisation : On donne les valeurs des
énergies de première ionisation pour les
éléments de la colonne du magnésium
: L'énergie de première ionisation est l'opposée de l'énergie orbitalaire de l'electron arraché ; c'est l'énergie qu'il faut fournir à l'atome, pris dans son état fondamental, pour arracher un électron externe. L'énergie de première ionisation diminue au sein d'une même famille quand n croît ; l'énergie de première ionisation diminue en descendant un groupe : les orbitales électroniques s'expandent de plus en plus lorsque le nombre quantique principal n augmente. Les électrons de valence occupent une région de l'espace de plus en plus lointaine du noyau et seront donc plus faciles à arracher à l'élément. Position des éléments en descendant la colonne : Be, Mg, Ca, Sr, Ba |
||||||||||||||
|
Les ions magnésium
Mg2+ réagissent en solution aqueuse avec
l'EDTA ( acide éthylène diamine
tétracétique ), noté H4Y (
pKa1 = 2,0 ; pKa2 = 2,7 ;
pKa3 = 6,1 ; pKa4 = 10,2) pour donner
un complexe stable MgY2- incolore. Domaine de prédominance des différentes formes de H4Y en fonction du pH
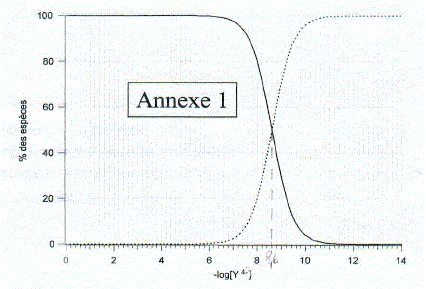
Equation de la réaction de formation de MgY2- : Mg2+ + Y4- = MgY2- Expression de la constante de formation du complexe que l'on notera bMg : bMg
= [MgY2-]
/([Mg2+][Y4-])
Identifier les deux espèces sur le graphe : log bMg = log ([MgY2-] /[Mg2+]) - log [Y4-]) = log ([MgY2-] /[Mg2+]) +pY log ([MgY2-] /[Mg2+]) = log bMg -pY = 8,6 -pY si pY<8,6 ( partie gauche du graphe annexe 1) alors log ([MgY2-] /[Mg2+])>0 et [MgY2-]>[Mg2+] si pY>8,6 ( partie droite du graphe annexe 1) alors log ([MgY2-] /[Mg2+])<0 et [MgY2-]<[Mg2+] Déterminer graphiquement bMg : à l'intersection des deux courbes [MgY2-] =([Mg2+] ; l'abscisse de l'intersection donne pY= 8,6 en conséquence bMg = 1 /[Y4-] : log bMg = - log [Y4-] = pY = 8,6 bMg
= 108,6 = 3,98
108.
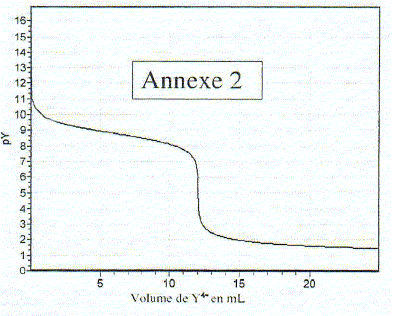
Points remarquables de la courbe : valeurs déduites. La brusque variation de pY correspond à l'équivalence :VE= 12 mL A la demi équivalence ( V= 6 mL Y4- ajouté ), MgY2-] =([Mg2+] : l'ordonnée de ce point permet de retrouver log bMg . Dosage d' une eau minérale : On souhaite doser une eau
minérale dont l'étiquette porte l'analyse
suivante :
Mg2+ : 7,5 mg/L ; M(Mg) = 24,3 g/mol d'où [Mg2+]= 7,5/ 24,3 = 0,309 mmol/L Ca2+ : 63,2 mg/L ; M(Ca) = 40,1 g/mol d'où [Ca2+]= 63,2/40,1 = 1,58 mmol/L C = [Mg2+] + [Ca2+] = 1,88 mmol/L = 1,88 10-3 mol/L A l'équivalence de ce dosage les quantités de matière des réactifs mis en présence sont en proportions stoechiomètriques : 50 *1,88 10-3 = 1,00 10-2 VE doù : VE = 5*1,88 = 9,4 mL.
|
||||||||||||||
|
|
||||||||||||||
|
Lors d'une séance de TP, on désire déterminer de façon indirecte l'enthalpie standart DrH° de la réaction de formation de l'oxyde de magnésium MgO à 298 K. Mg(s) + ½O2(g) =MgO(s) On utilise les réactions associées aux équations chimiques suivantes : Mg(s) + 2H+ = Mg2+ + H2(g) (1) DrH°1. MgO(s) + 2H+ = Mg2+ + H2O (2) DrH°2. H2(g) + ½O2(g) = H2O (3) DrH°3 = -285 kJ/mol Mode opératoire : - Préparation du calorimètre : on pèse un becher en verre mv=63,69 g ; on introduit dans le becher me = 125,00 g de solution d'acide chlorhydrique à 1,00 mol/L ; on place ensuite le becher préparé précédemment dans un calorimètre et on mesure la température initiale du système qi=19,4°C. - Expérience 1 : dans le becher précédent on introduit m1 = 0,51 g de tournure de magnésium Mg(s) ; on ferme le calorimètre, on agite puis on relève la température finale du système : qf 1=35,2°C. - Expérience 2 : dans un becher préparé de la même manière on introduit m2 = 1,00 g de magnésie MgO(s) ; on ferme le calorimètre, on agite puis on relève la température finale du système : qf 2=23,2°C. Données : on néglige la capacité thermique du calorimètre. - Chaleur massique de l'eau :
ce = 4,185 J g-1 K-1 ;
chaleur massique du verre : cv = 0,85 J
g-1 K-1 ; M( Mg ) = 24,31 g/mol ; M(O)
= 16,00 g/mol ; masse volumique de l'eau r=
1,00 103 kg m-3.
Le rôle du calorimètre : enceinte adiabatique, limitant considérablement les échanges thermiques avec le milieu extérieur. ( dans notre cas la différence de températures entre l'extérieur et l'intérieur du calorimètre est faible, et l'expérience est de courte durée : les échanges thermiques sont quasiment nuls ) La température finale est repérée lorsque l'équilibre thermique est atteint, en utilisant un thermomètre électronique donc la sonde de mesure passe à travers le couvercle du calorimètre et plonge dans le becher. La température finale est supérieure la température initiale du calorimètre et contenu. Approximations faîtes sur la chaleur massique et sur la masse volumique de la solution d'acide chlorhydrique : on assimile la chaleur massique et la masse volumique de la solution d'acide chlorhydrique à celles de l'eau, l'acide étant moyennement concentré. Catégorie de réactions : les réactions ( 1) et (2) sont des réactions d'oxydo-réductions Réaction (1) : Mg(s) est le réducteur, H+ est l'oxydant. Réaction (2) : MgO(s) est l'oxydant et H+ est le réducteur. Réactif en défaut pour la transformation (1) : Mg(s) + 2H+ = Mg2+ + H2(g) n0(Mg) = m/M= 0,51/24,31 = 2,1 10-2 mol ; n0(H+) = CV = 1*0,125 = 0,125 mol D'après les coefficients stoechiomètriques, 2,1 10-2 mol de magnésium nécessite 4,2 10-2 mol mol d'ion H+. Or on a mis 0,125 mol d'acide : donc l'acide est en exès et le magnésium en défaut. Réactif en défaut pour la transformation (2) : MgO(s) + 2H+ = Mg2+ + H2O n0(MgO) = m/M= 1/(24,31+16) = 2,5 10-2 mol ; n0(H+) = CV = 1*0,125 = 0,125 mol D'après les coefficients
stoechiomètriques, 2,5 10-2 mol de MgO
nécessite 5 10-2 mol mol d'ion
H+. Or on a mis 0,125 mol d'acide : donc l'acide
est en exès et l'oxyde de magnésium en
défaut. énergie gagnée par les corps froids : DrH°1=(mvcv+mece)(qf 1-qi)=(63,69*0,85+125*4,185) (35,2-19,4)=9,12 103 J à partir de 0,51 g Mg d'où par mol de magnésium : 9,12 103 *24,1/0,51 = 4,35 105 J/mol = 4,35 102 kJ/mol La transformation chimique (1) est donc exothermique : DrH°1 = - 4,35 102 kJ/mol. La transformation (2) étant totale, en déduire DrH°2 : DrH°2= énergie gagnée par les corps froids DrH°2=(mvcv+mece)(qf 2-qi)=(63,69*0,85+125*4,185) (23,2-19,4)=2,19 103 J à partir de1 g MgO d'où par mol de MgO : 2,19 103 *40,31 = 8,83 104 J/mol = 88,3 kJ/mol La transformation chimique (2) est donc exothermique : DrH°2 = - 88,3 kJ/mol. Valeur de DrH°, enthalpie standard de formation de MgO(s) : (1) + (3)-(2) donne Mg(s) + ½O2(g) =MgO(s) d'où : DrH° = DrH°1 + DrH°3 -DrH°2= - 435+ (-285) -(-88,3 )= - 632 kJ /mol.
|
||||||||||||||
|
|