L'objectif d'un microscope comprend - entre autre -
une lentille demi-boule; c'est une demi-sphère de
rayon R= 2 cm dont la coupe principale est
représentée ci-dessous :
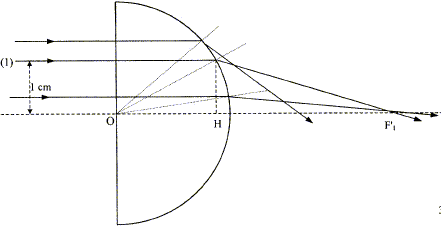
La lentille est constituée d'un verre d'indice
n1= 1,5 environ et se trouve dans l'air d'indice
n2 = 1. On considère un faisceau
monochromatique de rayons lumineux incidents se propageant
parallèlement à l'axe optique.
Cette lentille n'est pas une lentille mince :
l'épaisseur au centre n'est pas négligeable
devant le rayon de courbure ( ici e=R)
En conséquence, l'inconvénient majeur pour la
formation de l'image d'un objet situé à
l'infini est :
aberration géométrique (
sphérique) : un faisceau parallèle
incident ne converge pas en un point ; on observe une tache
étalée le long de l'axe optique principal.
L'image d'un objet étendu n'est pas nette.
Un diaphragme placé devant la lentille limite ce
phénomène en supprimant les rayons lumineux
trop écartés de l'axe optique
principal.
On considère le rayon lumineux incident se
propageant à un cm de l'axe optique
Calcul de OF'1 :
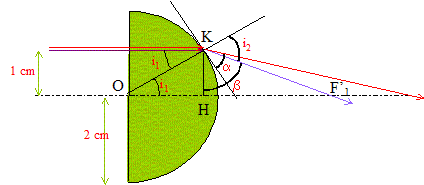
OF'1 = OH+HF'1 ; OH=
(OK2-HK2)½
=(2²-1²) ½ = 1,73 cm.
sin i1 = KH/OK= 0,5 ; i1 =
30°
loi de Descartes por la réfraction : 1*sin
i1 = 1,5 sin i2 soit i2 =
48,6 °;
a= 90-48,6 =41,4 ;
b= a+ i1
=71,4°
HF'1 = KH tan b=
2,97 cm ; d'où OF'1 =1,73+2,97 =
4,7 cm.
Le rayon incident est en fait constitué de deux
radiations, une rouge et une violette. Pour la radiation
rouge, l'indice de réfraction du verre est
n1r, différente de celle n1v de
la radiation violette.
Aberration chromatique : dispersion subie par la
lumière polychromatique réfractée par
le verre
Sachant que n1r = 1,5096 et n1v =
1,5264, je déterminer le rayon qui coupera l'axe
optique au plus près du point O.
|
indice
|
sin i2
|
i2
|
a =
90-i2
|
b= a+
i1
|
OF'1 =1,73+ tanb
|
|
n1r = 1,5096
|
1,5096 /2 = 0,7548
|
49°
|
41
|
71
|
4,63
|
|
n1v = 1,5264
|
1,5264 / 2 = 0,7632
|
49,74°
|
40,25°
|
70,25°
|
4,51.
|
retour
-menu