|
|
||
|
||
|
Le numéro atomique de l'élément sodium est Z=11. L'analyse du spectre d'émission d'une lampe à vapeur de sodium révèle la présence de raies de longueurs d'onde bien définies : 
structure électronique de l'élément sodium : 11 électrons dans l'état fondamental :1s2 2s2 2p6 3s1. domaine de longueurs d'ondeauquel appartiennent ces radiations : l1 < 400 nm donc domaine U V. l2 , l3 , l'3, l4 : domaine visible l5 , l6, valeurs supérieures à 800 nm : domaine I R. Calcul de la fréquence de la radiation jaune de longueur d'onde l3=589,0 nm = 5,89 10-7 m n = c/l3 =3 108 / 5,89 10-7 = 5,09 1014 Hz. Calcul de l'énergie ( en J et en eV) des photons correspondants :
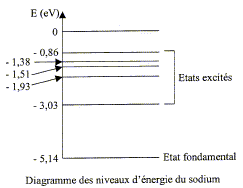
En utilisant le diagramme simplifié des niveaux d'énergie de l'atome de sodium, on trouve que l'écart énergétique entre le niveau excité n=1 et le fondamental vaut : -3,04+5,14 = 2,11 eV ; cette radiation jaune correspond donc à la transition de l'état excité 1 vers l'état fondamental. Un atome de sodium à l'état fondamental ne peut pas absorber un photon d'énergie 3 eV : l'énergie du photon doit être égale à la différence d'énergie entre un état excité et l'état fondamental.
|
||
|
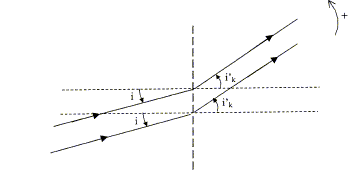
La formule des réseaux traduit le fait que dans la direction définie par sin ik' pour un angle i donné, les ondes diffractées par toutes les fentes sont en phase. n: nombre de traits par unité de longueur a=1 / n pas du réseau k appartient à Z, k est appelé l'ordre l longueur d'onde
(m) de la lumière
utilisée.
Calcul des angles ik' des directions dans lesquelles on a des maxima de lumière pour une radiation de longueur d'onde l = 589 nm. n = 750 traits / mm. le nombre de maxima principaux est fini : pour i =0 ( incidence normale); n =7,5 105 traits m-1 ; l=589 10-9 m sin ik' = kln soit sin ik' = 7,5 105 *589 10-9 k= 4,417 10-1 k k=0 donne
i0' =0 ; k =1 donne
i1' = + ou - 26,21°; k =2 donne
i2' = + ou - 62,06°.
Calcul de l'écart angulaire D ik' entre les directions ik' des maxima des radiations à l3 = 589 nm et l'3 =589,6 nm du spectre du sodium. sin
ik' = 7,5
105 *589,6 10-9 k= 4,422
10-1 k - à l'ordre k=2 :
i2' = + ou - 62,18°;
D ik' = 0,12
°
A l'ordre k=1, le pouvoir séparateur vaut : R= N= 7,5 105*0,02 = 1,5 104 traits utilisés ; l/Dlm
= 589 10-9 / 0,6 10-9 = 982 ; R >
l/Dlm
|
||
|
|