Aurélie nov 2001
précipitation et pH

hydroxyde d'aluminium

Google

L'hydroxyde d'aluminium est pratiquement insoluble ; pKs = 33. Cet hydroxyde est introduit dans l'eau pure.

  1. Les ions HO- issus de l'eau sont négligeables
    - Calculer la solubilté de l'hydroxyde .
    - Donner le pH de la solution et la solubilité de l'hydroxyde.
  2. L'hydroxyde Al(OH)3 comme l'ion Al3+ peuvent conduire au complexe [ Al(OH)4]- dont la constante de dissociation globale est pKd=35.
    - Pour une solution saturée, exprimer log [Al3+] et log [ [ Al(OH)4]- ] en fonction du pH.
    - Représenter graphiquement log [Al3+] et log [ [ Al(OH)4]- ] en fonction du pH.
    - Dans 1 L de solution on introduit 0,1 mol de chlorure d'aluminium AlCl3. Déterminer les concentrations des différentes espèces en solution ainsi que la quantité de matière Al(OH)3 précipité dans les cas suivants : pH=2 ; pH=4 ; pH=8 ; pH=13.
    - A quel pH la solubilité est-elle minimale ?
corrigé
Al(OH)3 en équilibre avec Al3+ + 3HO-.

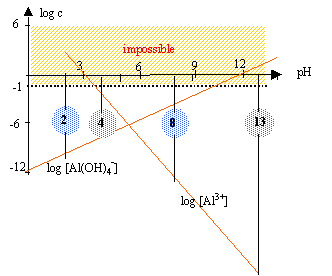
Ks = [Al3+] [HO-]3 = 10-33.

d'après les coefficients de l'équation ci-dessus : [HO-] = 3 [Al3+]

repport dans l'expression du produit de solubilité :

[HO-]4 = 3 10-33

[HO-] = 7,4 10-9 mol/L d'où s = [Al3+] = 2,47 10-9 mol/L

[H3O+] = 10-14 / 7,4 10-9 = 1,3 10-6 mol/L et pH =5,9.

autoprotolyse de l'eau :

Les valeurs précédentes sont fausses

lorsque 5,9 < pH < 8 il faut tenir compte des ions HO- et H3O+ issus de l'autoprotolyse de l'eau.

l'autoprotolyse de l'eau est dans ce cas la réaction prépondérante

2H2O en équilibre avec HO- + H3O+ avec Ke = 10-14 à 25°C et [H3O+] = [HO-]

[H3O+] [HO-] = [H3O+]² = 10-14 soit pH=7.

d'où s = [Al3+] =Ks /[HO-] 3= 10-33 / (10-7)3 = 10-12 mol/L.

équilibre de précipitation :

Al(OH)3 en équilibre avec Al3+ + 3HO-.

Ks = [Al3+] [HO-]3 = 10-33 = [Al3+] (10-14)3 / [H3O+]3.

log [Al3+] -42 -3 log [H3O+] = -33

log [Al3+] +3pH = 9 soit log [Al3+] =9-3pH.

 équilibre de complexation :

[ Al(OH)4]-en équilibre avec Al3+ + 4HO-.

Kd= [Al3+] [HO-]4 / [ Al(OH)4]-] = 10-35 = [Al3+] (10-14)4 / ( [H3O+]4[ Al(OH)4]-] )

log [Al3+] -56 -4 log [H3O+] -log[ Al(OH)4]-] = -35

log [Al3+] +4pH -log[ Al(OH)4]-] = 21

tenir compte de : log [Al3+] =9-3pH.

d'où 9+pH-log[ Al(OH)4]-] =21

log[ Al(OH)4]-] = -12 + pH.

pH
2
4
8
13
[Al3+] mol/L

10 9-3pH
0,1
10-3
10-15
10-30
[ Al(OH)4]-] mol/L

10 -12+pH
10-10
10-8
10-4
0,1
précipité (mol)
0
0,1-10-3 -10-8

= 0,0990
0,1-10-15 -10-4

= 0,0999
0
la solubilite totale s'écrit :

s = [Al3+] + [ Al(OH)4]-]

s = 10 9-3pH + 10 -12+pH

dériver par rapport à pH :

ds/dpH = -3 10 9-3pH + 10 -12+pH

dériver encore une fois :

d²s / dpH² = 910 9-3pH + 10 -12+pH toujours positive

donc la solubilité passe alors par un minimum lorsque la dérivée première s'annule

rechercher la valeur du pH qui annule cette dérivée.

-3 10 9-3pH + 10 -12+pH=0

3 10 9-3pH =10 -12+pH

prendre le logarithme de chaque membre

log 3 +9-3pH = -12 +pH

0,477 +21 = 4pH

pH = 5,37.

retour - menu