Aurélie 10/02
systèmes conjugués : méthode d'étude (Hückel)

Google

Comment appliquer la méthode de Hückel ?
  1. Repérer et numéroter les atomes du système conjugué.
  2. Ecrire le déterminant séculaire et le résoudre.
  3. Construire le diagramme des orbitales moléculaires p.
  4. Repérer les OM liantes, antiliantes, placer les électrons, représenter les OM.
  5. Evaluer l'énergie de résonance, l'indice des liaisons.
Comment reconnaître un système conjugué ?

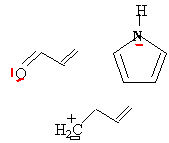
Un tel système est constitué d'atomes dont les oprbitales p se recouvrent latéralement. Cela nécessite que les atomes soient coplanaires.

En dehors d'une suite ininterrompues de double liaison >C=C< il faut ausi penser aux hétéroatomes.

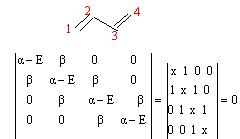
simplifier le déterminant séculaire : ( système C et H )

les simplifications :

  1. Toutes les intégrales coulombiennes ont la même valeur notée a.
  2. Toutes les intégrales de résonance valent b pour deux atomes liés sinon zéro.
  3. Les intégrales de recouvrement valent 1 si i = j sinon zéro.
  4. On utilise la variable x = (a-E) / b ( E étant l'énergie des OM)

exemple du butadiéne :

la résolution donne x4-3x2+1=0

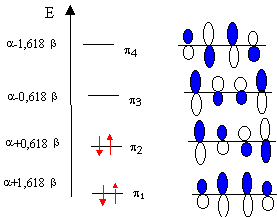
soit x1 = 1,618 ; x2 = 0,618 ;x3 = -0,618 ; x4 = -1,618 ;

quant aux énergies des OM :

E1 = a+1,618 b ; E2 = a +0,618 b ; E3 =a -0,618 b ; E4 = a -1,618 b;

déterminer les coefficients des OM :

pour x= -1,618 résoudre le système d'équations suivant :

-1,618 c1 + c2 = 0 (1) donne c2 =1,618 c1 ( repport dans (2))

c1-1,618c2+c3=0 (2) donne c3 = 1,618 c1 (repport dans(4))

c2-1,618c3+c4=0 (3)

c3-1,618 c4=0 (4) donne c1=c4

condition de normation c1²+c2²+c3²+c4²=1

mêmes calculs pour les autres valeurs de x. 

exploiter les résultats :

la première colonne du tableau donne les énergies des OM ( b <0) et les colonnes suivantes donnent la part de chaque OA dans l'OM.
énergie
p1
p2
p3
p4
a+1,618 b
0,372
0,602
0,602
0,372
a +0,618 b
0,602
0,372
-0,372
-0,602
a -0,618 b
0,602
-0,372
-0,372
0,602
a -1,618 b
0,372
-0,602
0,602
-0,372
On dessine les lobes (plus le coefficient est grand, plus le lobe est de grande taille)

On colorie par exemple le lobe inférieur quand le coefficient est négatif. et le lobe supérieur si le coefficient est positif

calcul de l'énergie de résonance :

c'est la différence d'énergie d'un système (hypothétique ) de doubles liaisons isolées d'énergie 2(a+b) ( énergie d'une double liaison à deux électrons) et l'énergie électronique du système conjugué en kJ/mol

Erésonance = 4(a+b) - 2 (a+1,618b)-2(a+0,618b) = -0,472 b (valeur positive car b <0)

calcul de l'indice de liaison :

il représente la force de la liaison entre deux atomes noté j et k

pjk=Si ni Cij Cik.

p12 = p34 = 2(0,372*0,602)+2(0,602*0,372)= 0,896.

p23 =2(0,602*0,602)+2(0,372-(-0,372))= 0,448

calcul de l'a charge électronique totale d'une molécule

qj=Si ni Cij2.

q1 =q2 = q3 = q4 = 2*0,602²+2 0,372² = 1

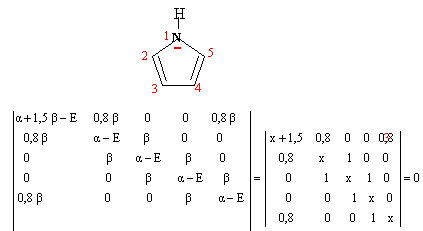
introduire les héteroatomes dans le déterminant :

on remplace a par a+kb et b par hb

h et k dépendent de l'héteroatome et valent k=1,5 et h=0,8 pour un atome d'azote.

retour - menu