Un réveil en douceur : bobine inductive bac S France 2008.

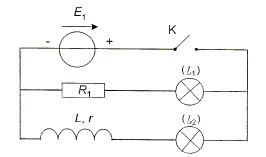
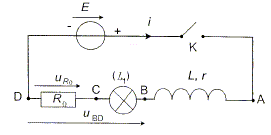
Lorsque l'heure du réveil est atteinte, une lampe diffuse une lumière dont l'intensité lumineuse augmente progressivement jusqu'à une valeur maximale. On évite ainsi un réveil trop brutal. La durée nécessaire pour atteindre la luminosité maximale est modifiable. Influence d'une bobine dans un circuit électrique. Un circuit est constitué d'une source de tension idéale de fem E1, d'une bobine d'inductance L et de résistance r, d'un conducteur ohmique de résistance R1 de même valeur que r et de deux lampes identiques. E1 = 24 V ; L= 1 H ; r = R1 = 7 W. On suppose que chaque lampe a le même comportement électrique qu'un conducteur ohmique de résistance Rlampe.   Immédiatement après la fermeture de l'interrupteur K, les deux lampes ne s'allument pas simultanément : une lampe brille quasi-instantanément, l'autre brille avec retard. Quelle lampe s'allume la première ? Pourquoi l'autre s'allume-t-elle avec retard ? La lampe L1 en série avec le conducteur ohmique R1 s'allume la première. La bobine inductive introduit un retard à l'établissement du courant dans la branche contenant la lampe L2 : celle-ci s'allume avec retard. Dans la branche du circuit contenant la bobine, on peut observer successivement deux régimes différents pour le courant électrique. Nommer ces deux régimes. Régime transitoire : la lampe L2 brille progressivement. Régime permanent : la luminosité de cette lampe L2 est constante. Que peut-on dire de la luminosité des deux lampes en fin d'expérience ? Justifier. 1er point : les deux lampes sont identiques. 2ème point : en régime permanent, la bobine inductive se comporte comme un conducteur ohmique de résistance r. 3ème point : les lampes sont en série avec des résistors identiques. En conséquence, la luminosité finale des lampes est identique. On appelle t la constante de temps caractérisant l'évolution temporelle de l'intensité du courant électrique lors de l'association en série d'un conducteur ohmique de résistance R et d'une bobine d'inductane L. Dans le cas étudié R= R1+Rlampe. La durée nécessaire pour atteindre la luminosité maximale est de l'ordre de 5t. Donner l'expression de t. t = L/R. Vérifier par analyse dimensionnelle que t est homogène à un temps. énergie = ½L i2 ; L est une énergie divisée par une intensité au carré : L s'exprime en J A-2. énergie ( effet Joule) = Ri2t ; R est une énergie divisée par un temps et par une intensité au carré. R s'exprime en J A-2 s-1. Par suite L/ R s'exprime en seconde : t est homogène à un temps.   Web www.chimix.com   Justifier par un calcul d'ordre de grandeur le fait que le phénomène est détectable par un observateur. On prendra R~ 10W. 5t =L/R 5*1/10 5t = 0,5 s : de l'ordre de la seconde L'oeil étant capable de distinguer deux images consécutives séparées d'au moins 0,1 s, le phénomène est détectable. 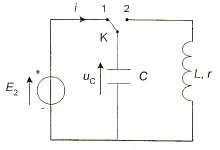Vérification de la valeur de l'inductance de la bobine. On réalise le montage ci-dessous permettant d'enregistrer la décharge d'un condensateur de capacité C= 22 mF à travers la bobine. 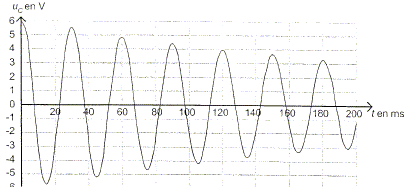Le condensateur est initialement chargé sous une tension E2= 6,0 V ( commutateur en position 1) Après avoir basculé le commutateur en position 2, on enregistre l'évolution de la tension aux bornes du condensateur au cours du temps. Comment nomme t-on le régime correspondant à cette évolution de la tension uC aux bornes du condensateur ? pseudo-périodique Quelle est la cause, en terme d'énergie, de l'amortissement des oscillations ? Au cours des échanges d'énergie entre condensateur et bobine, une partie de l'énergie est dissipée sous forme de chaleur ( effet Joule) dans les parties résistives ( résistance r de la bobine). Qualifiée l'évolution temporelle de l'énergie totale emmagasinée dans le circuit en choisissant un oiu plusieurs adjectifs parmi : périodique, croissante, décroissante, sinusoïdale. 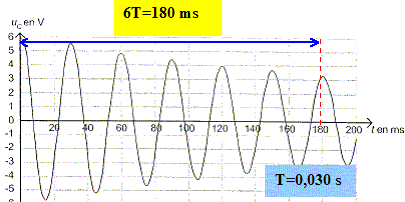décroissante Déterminer la valeur de la pseudo-période T puis l'inductance de la bobine. Conclure. La pseudo-période T est voisine de la période T0 du dipole LC si l'amortissement est faible. T0 =2p[LC]½ : L=T20 /(4p2C) 0,032 /(4*3,142*22 10-6) L=1,0 H Valeur en accord avec celle qui est donnée.   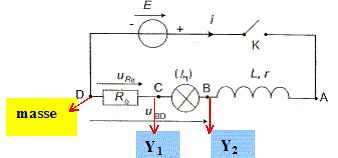Etude expérimentale de la luminosité d'une lampe dans un circuit inductif.    La luminosité de la lampe est liée à la puissance électrique qu'elle reçoit. La puissance instantanée reçue par un dipôle soumis à une tension u(t) et traversé par un courant i(t) est : p(t) = u(t) i(t). Pour étudier l'évolution temporelle de cette puissance, on réalise le montage ci-dessous et on procède à une acquisition informatique des données. On utilise la lampe L1, la bobine d'inductance L, un conducteur ohmique de résistance R0=1 W et une source de tension continue de fem E. De quelle(s) manière(s) l'énergie reçue par la lampe est-elle transférée à l'environnement ? énergie thermique ( chaleur) et rayonnement A quels points du circuit ( A, B, C ou D) faut-il brancher les voies Y1 , Y2 et la masse M de l'interface pour enregistrer les tensions uR1 et uBD ? 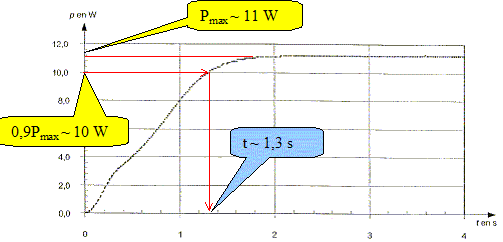A partir des grandeurs mesurées uR0, uBD et de la résistance R0 : exprimer la tension u(t) = uBC, l'intensité i(t) du courant électrique et la puisance p(t) reçue par la lampe. uR0 = R0 i(t)   : i(t) = uR0/ R0. Additivité des tensions : uBD = uR0 + uBC ; u(t) =uBC = uBD - uR0. p(t) = u(t) * i(t) ; p(t) = (uBD - uR0)uR0/ R0. Pourquoi les élèves ont-ils choisi un conducteur ohmique dont la résistance est très faible ? 1er point : l'éclairement de la lampe doit être important en régime permanent : l'intensité du courant doit donc être assez grande. 2ème point : en régime permanent la bobine se compoerte comme u conducteur ohmique de résistance r. 3ème point : en régime permanent, la résistance totale du circuit est Rtotale = r+R0+Rlampe ; I= E/ Rtotale. L'intensité sera d'autant plus grande ( grande luminosité) que R0 sera plus petite. La figure ci-dessous représente l'évolution temporelle de la puissance électrique p(t) reçue par la lampe. On estime que pour pouvoir réveiller un individu, la lumière est suffisante lorsque la puissance atteint 90 % de sa valeur maximale. Déterminer la durée nécessaire pour permettre le réveil. Cette durée est-elle compatible avec l'utilisation d'un tel montage pour une lampe " à diffusion douce " ? Quels paramètre faudrait-il modifier pour contrôler la durée du phénomène ? Le réveil est trop brutal ( 1,3 s) : ce montage est incompatible avec une lampe " à diffusion douce ". La durée étant proportionnelle à L et inversement proportionnelle à Rtotale, on peut augmenter cette durée en : augmentant l'inductance L ; en diminuant la résistance Rtotale.

retour -menu