Aspect énergétique de la décharge d'un condensateur.

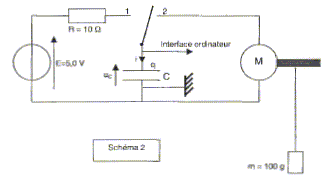
Restitution de l'énergie et décharge à courant constant : On prendra C= 1,0 F. Le condensateur est incorporé au montage suivant : M est un moteur sur lequel est enroulé une ficelle soutenant à son extrémité une masse m= 100 g. A l'instant t=0, pris comme nouvelle origine des temps, on bascule l'interrupteur en voie 2. Le condensateur se décharge et le moteur se met en mouvement entraînant la charge m =100 g. Celle-ci monte d'une hauteur h= 3,10 m en 18 s. Les valeurs enregistrées par le logiciel sont les suivantes : t=0 ( démarrage du moteur) ; uC(0)=4,9 V ; t=18 s ( arrêt du moteur), uC(18)= 1,5 V. L'enregistrement de uC(t) par le logiciel donne une courbe qui peut être assimilée à une droite représentée par uC(t) = a t+b avec a<0 et b>0. Calculer les valeurs numériques des constantes a et b. t=0 ( démarrage du moteur) ; uC(0)=4,9 V uC(0)=4,9 =a*0 + b ; b= 4,9 V. t=18 s ( arrêt du moteur), uC(18)= 1,5 V uC(18)= 1,5 = a*18+4,9 ; a = -0,19 V s-1. uC= -0,19 t + 4,9. Déterminer l'expression de la charge instantanée q(t) du condensateur en fonction du temps. q(t) = C uC(t) avec C= 1,0 F ; q(t) = -0,19 t +4,9. En déduire la valeur de l'intensité du courant i. i(t) = dq(t) / dt i(t) = dq(t) / dt = -0,19 A. Que pensez-vous du signe de i ? Le signe moins traduit le fait que le courant a le sens contraire du courant de charge.     Web www.chimix.com Calculer successivement : - l'énergie stockée dans le condensateur à t=0. E = ½CUc2 ½CUc2(0) = 0,5*4,92 = 12 J. - l'énergie restant à t = 18 s. ½CUc2(18) = 0,5*1,52 = 1,1 J - l'énergie cédée par le condensateur. ½CUc2(0) -½CUc2(18) =10,87 J ( réponse 11 J) - l'énergie mécanique '( potentielle) reçue par la masse ( g= 9,8 m/s²) Epot =mgh mgh = 0,1*9,8*3,1 = 3,0 J. - le rendement du dispositif. énergie mécanique potentielle / énergie cédée par le condensateur *100 = 3/10,87 *100 = 28 %.

retour -menu