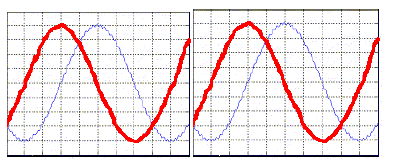
Ondes mécaniques : la houle, milieu dispersif.

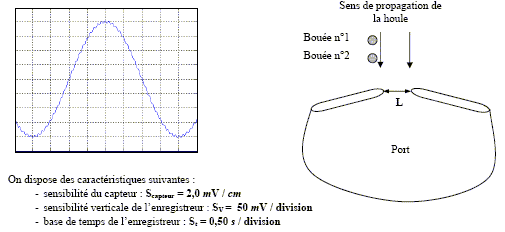
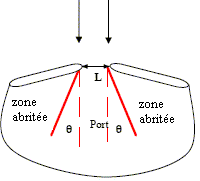
étude de la houle Un capteur fixé sur la bouée n°1 permet d'enregistrer le mouvement vertical de la surface de la mer dû à la houle. Ce capteur a permis de réaliser l'enregistrement présenté ci-dessous, débutant à un instant choisi comme origine ( t=0). Comment nomme-t-on plus couramment la “période spatiale” d’une onde ? Quelle est la période (temporelle) de cette houle ? On observe que l’écart d entre les sommets de deux vagues successives est de 24 m. Quelle est la vitesse de propagation de cette houle ? Quelle est l'amplitude de cette houle ? Sur les grilles quadrillées fournies ci-dessous, représenter : - L'enregistrement qu'on aurait obtenu si le capteur avait été déclenché à l'instant t1=3 s. - L'enregistrement qu'on aurait obtenu avec un second capteur placé sur la bouée n°2 située à une distance de 6 m de la première dans le sens de propagation de la houle. La houle atteint l'entrée d'un port, limité par deux digues séparées par un passage de largeur L=48 m. - Quel phénomène se produit-il ? - Quelle est la zone du port qui ne sera pas abritée de la houle ? Représenter qualitativement cette zone sur le schéma, et préciser la relation qui permet de calculer l'angle q correspondant à la limite entre la zone abritée et la zone non abritée. Calculer q. corrigé “période spatiale” d’une onde : longueur d'onde exprimée en m. période (temporelle) de cette houle : lecture graphe : 8 divisions soit T= 8*0,5 = 4 s.  vitesse de propagation de cette houle : longueur d'onde l=24 m v = l/T= 24/4 = 6 m/s. amplitude de cette houle : lecture graphe : 8 divisions crête à crête soit 2A= 8*0,05 = 0,4 V = 400 mV puis prendre en compte la sensibilité du capteur 2 mV/cm d'où : 2A=200 cm = 2 m ; A= 1,0 m capteur déclenché à l'instant t1=3 s ; enregistrement avec un second capteur : phénomène se produisant à l'entrée du port dont la largeur est du même ordre de grandeur que la longueur d'onde : diffraction    q= l/L =24/48 = 0,5 rad     Web www.chimix.com  La houle On s'intéressera dans cet exercice à l'étude de la houle en haute mer, à savoir en eau profonde, et aux caractéristiques de celle-ci en fonction d'une échelle en intensité appelée échelle de Beaufort. Dans une revue maritime traitant du sujet, on peut lire le texte suivant : Lorsque le vent souffle sur une mer calme, le frottement de l'air crée de petites rides puis des vaguelettes et enfin des vagues à mesure que la vitesse du vent augmente. L'ensemble de ces vagues, généré sur un intervalle de temps plus ou moins long, constitue la houle. Cette houle peut être décrite à l'aide de trois paramètres. - La hauteur h, définie comme la distance verticale entre le sommet de la crête et le fond du creux de la vague. - La longueur L, comme la distance entre deux crêtes ou deux creux successifs. - La cambrure, définie comme le rapport de sa hauteur sur sa longueur - La cambrure, définie comme le rapport de sa hauteur sur sa longueur. Ainsi le phénomène de la houle peut être considéré comme une onde mécanique. Aussi on assimilera dans tout l'exercice la houle à une onde progressive périodique sinusoïdale rectiligne dont les paramètres caractéristiques peuvent varier suivant l'état de la mer. 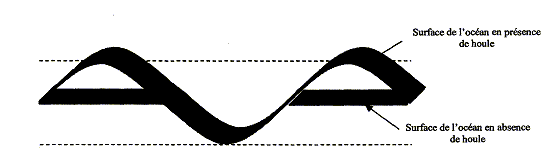Le schéma ci-dessus représente la surface de l'eau affectée par la houle à un instant donné. Placer sur ce schéma les paramètres " hauteur " et " longueur" A quelle grandeur spatiale, caractéristique d'un phénomène ondulatoire, est associé le terme "longueur " du texte d'introduction ? Quelle est sa définition ? Quelle grandeur temporelle permet de caractériser une onde mécanique ? Quelle est sa définition ?   L'échelle de Beaufort établie en 1805 - du nom de l'amiral de la marine britannique Francis Beaufort - graduée de 0 à 12 permet de caractériser la vitesse des vents. L'état de la mer étant directement lié à la vitesse du vent, cette échelle permet également de caractériser l'état de la mer et donc les conditions de navigation. Le tableau ci-dessous présente les derniers degrés d'une échelle de Beaufort simplifiée que le candidat utilisera dans la suite de l'exercice. On se place dans le cas où la cambrure des vagues notée Ca est telle que Ca = 1/7. On gardera cette valeur de cambrure pour tout le reste de l'exercice. échelle de Beaufort simplifiée degré sur l'échelle hauteur de la houle en mètre 5 2,0 6 3,0 7 4,0 8 5,5 9 7,0 10 9,0 11 11,5 12 14,0 Donner l'expression reliant la hauteur h des vagues, leur longueur L et leur cambrure Ca. Déterminer alors la longueur des vagues pour les degrés 6, 8, 10 et 12 de l'échelle de Beaufort. On placera les valeurs dans le tableau suivant : échelle de Beaufort 5 6 7 8 9 10 12 12 hauteur h de la houle(m) 2,00 3,00 4,00 5,00 7,00 9,00 11,5 14,0 longueur L (m) 14,0 28,0 49,0 80,5 période T(s) 2,10 2,60 3,00 3,50 4,00 4,50 5,10 5,60 célérité (m/s) 6,67 8,08 11,0 12,3 15,8 17,5 - Donner l'expression reliant la longueur L, la célérité v de l'onde et sa période T. - En déduire l'expression reliant la longueur L, la célérité v et la fréquence f de l'onde associée. - Le tableau fourni ci-dessus donne également les périodes associées aux différents degrés de l'échelle. Pour les degrés 7 et 10 de l'échelle de Beaufort déterminer la célérité v de l'onde associée. On donne la courbe traduisant l'évolution v2=f (L). - Quel est le type de courbe obtenue ? Quelle expression mathématique simple relie alors le carré de la célérité à la longueur ? -Calculer alors le coefficient k caractéristique de cette relation. On précisera l'unité de cette grandeur. Rappeler la définition d'un milieu dispersif. 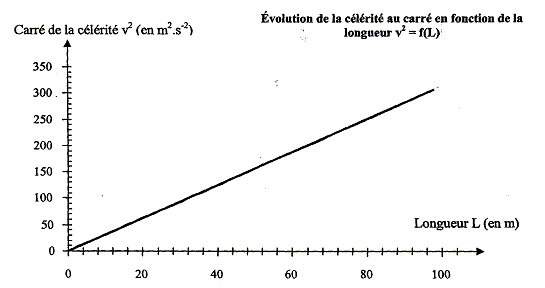- Déterminer l'expression littérale reliant la célérité v de la houle à sa fréquence f. - Conclure quant à la nature dispersive de ce milieu. corrigé 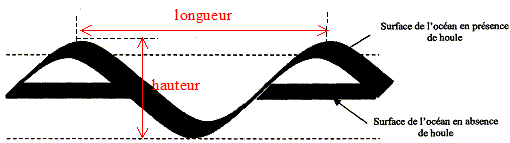le terme "longueur " du texte d'introduction est associé à la période spatiale, ou longueur d'onde, distance séparant deux crêtes consécutives. définition de la longueur d'onde : plus petite distance séparant deux points du milieu se trouvant dans le même état vibratoire. La période temporelle, inverse de la fréquence, permet de caractériser une onde mécanique. définition de la période temporelle : plus petite durée au bout de laquelle un point du milieu se retrouve dans le même état vibratoire. La cambrure, définie comme le rapport de sa hauteur sur sa longueur : Ca = h/L longueur des vagues pour les degrés 6, 8, 10 et 12 de l'échelle de Beaufort : L= h/Ca = 7 h. échelle de Beaufort 5 6 7 8 9 10 12 12 hauteur h de la houle(m) 2,00 3,00 4,00 5,00 7,00 9,00 11,5 14,0 longueur L (m) 14,0 21,0 28,0 35,0 49,0 63,0 80,5 98,0 expression reliant la longueur L, la célérité v de l'onde et sa période T : L= vT expression reliant la longueur L, la célérité v et la fréquence f de l'onde : L= v/f célérité v de l'onde associée : v = L/T échelle de Beaufort 5 6 7 8 9 10 12 12 longueur L (m) 14,0 21,0 28,0 35,0 49,0 63,0 80,5 98,0 période T(s) 2,10 2,60 3,00 3,50 4,00 4,50 5,10 5,60 célérité (m/s) 6,67 8,08 9,33 11,0 12,3 14,0 15,8 17,5 type de courbe : droite passant par l'origine : v² et L sont proportionnelles ; v² = k L avec k une constante égale au coefficient directeur de la droite. k = 310/ 100 = 3,1 m s-2. définition d'un milieu dispersif : dans un milieu dispersif la célérité des ondes dépend de leur fréquence. expression littérale reliant la célérité v de la houle à sa fréquence f : v² = 3,1 L avec L= l ( longueur d'onde) ; de plus l = v/f d'où : v² = 3,1 v/f soit v= 3,1/f La vitesse dépend de la fréquence ; en conséquence ce milieu est dispersif.

retour -menu