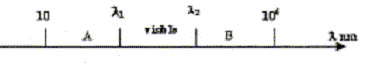Ondes
électromagnétiques
- Le spectre des ondes électromagnétiques
est partagé en plusieurs parties.
- Pour chacun des domaines A et B donner son nom.
- Donner les valeurs des longueurs d'ondes
l1 et l
2.
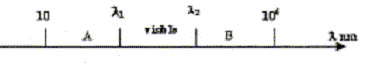
- On considère une onde de fréquence
n= 640 1012 Hz. A
quelle vitesse se déplace-t-elle dans le vide
?
- A quel domaine appartient cette onde ? Justifier.
- On envisage le passage de cette onde dans un milieu
d'indice n= 1,5. Déterminer sa vitesse dans ce
milieu.
- La fréquence de l'onde est-elle
différente dans le milieu d'indice n ? Si oui
préciser si elle est plus petite ou plus grande ?
Même question pour la longueur d'onde.
- Proposer une source de lumière
monochromatique.
corrigé
domaine A : infrarouge (IR) ; domaine B :
ultraviolet (UV)
longueurs d'ondes
l1 : 800 nm et l
2 = 400 nm
une onde de fréquence n=
640 1012 Hz se déplace dans le vide
à la célérité de la
lumière c = 3 108 m/s.
domaine auquel appartient cette onde : l
= c/n =3
108 /640 1012 =4,7 10-7 m =
470 nm, valeur comprise entrel1
et l 2,
donc domaine "visible".
vitesse de l'onde dans le milieu d'indice n=1,5 : c/n=3
108/1,5 =2 108 m/s.
La fréquence de l'onde caractérise l'onde :
elle reste constante quel que soit le milieu traversé
par l'onde.
|
|
l =
c/n : n
étant constant, la
célérité c dépend du
milieu , donc la longueur d'onde dépend du
milieu traversé ; dans ce milieu d'indice n
la longueur d'onde diminue et vaut l
0/n, l
0 longueur d'onde dans le vide.
La lumière "laser" est une source de
lumière monochromatique.
|
|
|
La
lumière : une onde
Huyghens (1629-1695) donne à la
lumiére un caractére ondulatoire par
analogie à la propagation des ondes à
la surface de l'eau et à la propagation du
son.
Pour Huyghens, le caractère ondulatoire
de la lumière est fondé sur les faits
suivants:
- " le son ne se propage pas dans une enceinte
vide d'air tandis que la lumière se propage
dans cette même enceinte. La lumière
consiste dans un mouvement de la matière qui
se trouve entre nous et le corps lumineux,
matière qu'il nomme éther".
- " la lumière s'étend de toutes
parts1 et, quand elle vient de
différents endroits, même de tout
opposés2 , les ondes lumineuses
se traversent l'une l'autre sans
s'empêcher3 "
- " la propagation de la lumière depuis
un objet lumineux ne saurait être4
par le transport d'une matière, qui depuis
cet objet s'en vient jusqu'à nous ainsi
qu'une balle ou une flèche traverse l'air
".
Fresnel (1788-1827) s'attaque au problème
des ombres et de la propagation rectiligne de la
lumière.
Avec des moyens rudimentaires, il
découvre et il exploite le
phénomène de diffraction.
Il perce un petit trou dans une plaque de
cuivre. Grâce à une lentille
constituée par une goutte de miel
déposée sur le trou, il concentre les
rayons solaires sur un fil de fer.
Extraits d'articles parus dans l'ouvrage "
Physique et Physiciens " et dans des revues "
Sciences et Vie ".
1 de toutes parts = dans toutes
les directions ; 3 sans s'empêcher
= sans se perturber
2 de tout opposés = de
sens opposés ;4 ne saurait
être = ne se fait pas
I. Questions à
propos du document
- Texte concernant Huyghens
- Quelle erreur commet Huyghens en comparant la
propagation de la lumière à celle
des ondes mécaniques ?
- Citer deux propriétés
générales des ondes que l'on peut
retrouver dans le texte de Huyghens.
Texte concernant Fresnel
- Fresnel a utilisé les rayons solaires pour
réaliser son expérience. Une telle
lumière est-elle monochromatique ou
polychromatique?
- Fresnel exploite le phénomène de
diffraction de la lumière par un fil de fer.
Le diamètre du fil a-t-il une importance
pour observer le phénomène de
diffraction? Si oui, indiquer quel doit être
l'ordre de grandeur de ce diamètre.
corrigé
:
La lumière se propage dans le vide alors
que les ondes mécaniques et sonores ont
besoin d'un milieu matériel pour se
propager.
Les ondes transportent de l'énergie sans
transport de matière.
Les ondes se propagent de proche en proche
à partir de la source dans toutes les
directions qui lui sont offertes.
La lumière solaire est polychromatique.
Le diamètre du fil doit être du
même ordre de grandeur que la longueur d'onde
de la lumière ( de quelque microns à
quelques dizaines de microns)
|
II. Diffraction
:
On réalise une expérience de diffraction
à l'aide d'un laser émettant une
lumière monochromatique de longueur d'onde
l.
A quelques centimètres du laser, on place
successivement des fils verticaux de diamètres
connus. On désigne par a le diamètre d'un fil.
La figure de diffraction obtenue est observée sur un
écran blanc situé à une distance D =
1,60 m des fils. Pour chacun des fils, on mesure la largeur
L de la tache centrale. À partir de ces mesures et
des données, il est possible de calculer
l'écart angulaire q du
faisceau diffracté (voir figure 1
ci-après).
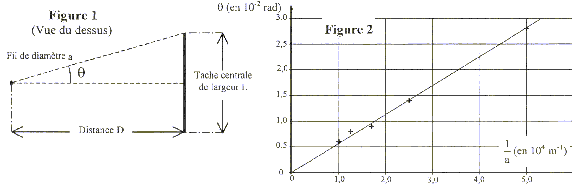
- L'angle q étant
petit, q étant
exprimé en radian, on a la relation: tan
q voisin q.
Donner la relation entre L et D qui a permis de calculer
q pour chacun des fils.
- Donner la relation liant q,
l et a. Préciser les
unités de q,
l et a.
- On trace la courbe q
=f(1/a). Celle-ci est donnée sur la figure 2
ci-dessus : Montrer que la courbe obtenue est en accord
avec l'expression de q
donnée à la question
précédente.
- Comment, à partir de la courbe
précédente, pourrait-on déterminer
la longueur d'onde l de la
lumière monochromatique utilisée ?
- En utilisant la figure 2, préciser parmi les
valeurs de longueurs d'onde proposées ci-dessous,
quelle est celle de la lumière utilisée.
560 cm ; 560 mm ; 560 µm ; 560 nm
Si l'on envisageait de réaliser la même
étude expérimentale en utilisant une
lumière blanche, on observerait des franges
irisées. En utilisant la réponse donnée
à la question 2.2., justifier succinctement l'aspect
"irisé" de la figure observée.
corrigé
:
D'après la figure : tan q
= ½L/D voisin de q en
radian.
De plus
: q
=
l/a
; q en radian;
l et a en mètre.
en traçant la courbe q
= f(1/a) on obtient une droite de coefficient directeur
égal à l.
coef. directeur = 2,8 10-2 / 5 104
= 2,8 10-6 / 5 = 0,56 10-6 m = 560 nm
= 0,56 mm.
Chaque radiation de la lumière polychromatique
donne un système de diffraction dont la largeur de la
tache centrale est proportionnelle à la longueur
d'onde. A centre de la tache toutes les radiations sont
présentes ( couleur blanche) ; le bord de la tache
centrale est orange-rouge, le bleu étant absent : la
longueur d'onde du bleu est plus petite que celle du
rouge.
III.
Dispersion
:
Un prisme est un milieu dispersif : convenablement
éclairé, il décompose la lumière
du faisceau qu'il reçoit.
- Quelle caractéristique d'une onde lumineuse
monochromatique est invariante quel que soit le milieu
transparent traversé ?
- Donner la définition de l'indice de
réfraction n d'un milieu homogène
transparent, pour une radiation de fréquence
donnée.
- Rappeler la définition d'un milieu dispersif.
Pour un tel milieu, l'indice de réfraction
dépend-il de la fréquence de la radiation
monochromatique qui le traverse?
À la traversée d'un prisme, lorsqu'une
lumière monochromatique de fréquence
donnée passe de l'air (d'indice na = 1)
à du verre (d'indice nv> 1), les angles
d'incidence (i1) et de refraction
(i2), sont liés par la relation de
Descartes-Snell: sin(i1) = nv*
sin(i2). Expliquer succinctement, sans calcul, la
phrase " Un prisme est un milieu dispersif': convenablement
éclairé, il décompose la lumière
du faisceau qu'il reçoit ".
corrigé
:
La fréquence ( en hertz Hz) caractérise une
onde : c'est un invariant.
L'indice de réfraction d'un milieu transparent,
noté n ( n supérieur à 1) est
égal au rapport de la célérité
de la lumière dans le vide ( 3 108 m/s)
à la célérité de la
lumière dans le milieu transparent.
Un milieu est dispersif lorsque la
célérité de l'onde en propagation dans
ce milieu dépend de sa fréquence.
L'indice de réfraction dépend de la
célérité donc de la fréquence de
l'onde.

sin i2 = sin (i1 ) /
nv.
L'angle i2 est d'autant plus grand que
i1 est grand : éclairé le prisme
sous incidence rasante ( i1 proche de
90°).
L'indice du verre dépend de la fréquence :
la lumière blanche est polychromatique ; le bleu est
plus dévié que le rouge à la
traversée du prisme.
|