Ondes mécaniques progressives : ondes sonores, ultrasons.

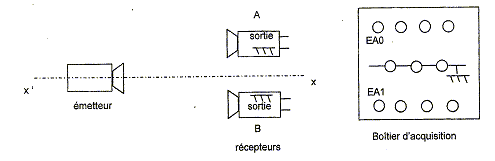
Généralités sur les ondes sonores. Donner la définition d'une onde mécanique progressive. Propagation d'une perturbation dans un milieu matériel avec transport d'énergie, sans transport de matière. Les ondes sonores sont un exemple d'ondes mécaniques. Pourquoi une éventuelle communication par onde sonore entre la Terre et la Lune ne serait-elle pas possible ? Une onde mécanique a besoin d'un milieu matériel pour se propager ; or entre la terre et la lune il y a le vide : une communication par onde sonore est donc impossible. Donner un exemple d'onde pouvant se propager dans le vide. Ondes électromagnétiques : la lumière par exemple. Dans le cas d'une onde sonore, la direction de la perturbation est parallèle à celle de la direction de la propagation. Comment peut-on alors qualifier ces ondes ? longitudinales. Détermination de la célérité des ultrasons : 1ère méthode. On alimente un émetteur d'ultrasons en mode " Salve ". 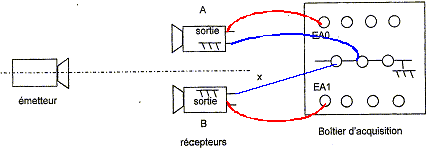On place face à l'émetteur deux récepteurs A et B comme indiqué sur le schéma simplifié du montageci-dessous. 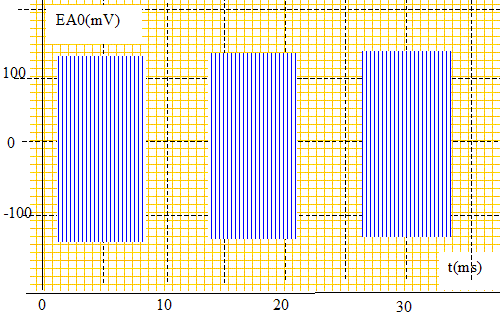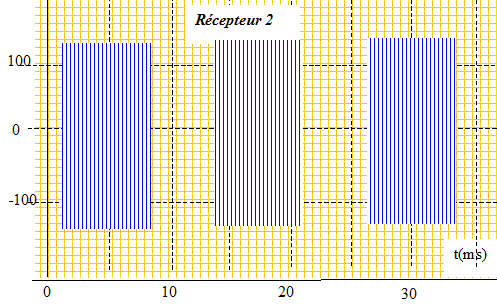Le récepteur A est relié à la voie EA0 du boîtier d'acquisition, le récepteur B à la voie EA1. 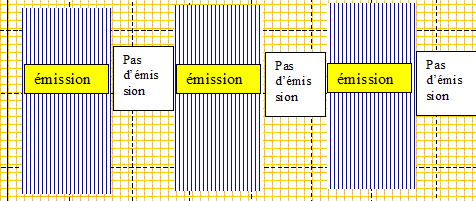L'enregistrement est présentéci-dessous. La fenêtre 1 correspond au récepteur A, la fenêtre 2 correspond au récepteur B. Compléter le schéma simplifié du montage en y faisant apparaître les branchements vers le boîtier d'acquisition. Identifier et indiquer dans la fenêtre 1, les zones d'émission sonore et les zones sans émission. L'amplitude de la tension est nulle quand il n'y a pas d'émission d'ultrasons. Positionner les salves de l'acquisition obtenue dans la fenêtre 2 ( récepteur n°2). Les deux récepteurs sont à la même distance de l'émetteur : les salves reçue par l'émetteur 2 sont identiques à celles reçues par l'émetteur 1. Les amplitudes sont identiques et on observe aucun décalage.       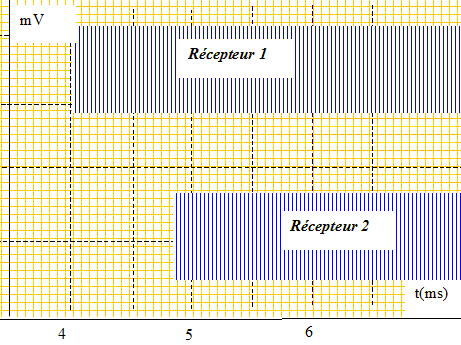Web www.chimix.com On déplace ensuite le récepteur B, dans la direction émetteur-récepteur, d'une distance d suffisamment grande pour pouvoir mesurer avec précision le retard ultrasonore Dt correspondant au passage de l'onde par les deux récepteurs. Le déplacement s'effectue selon un axe parallèle à l'axe x'x du schéma simplifié du montage. 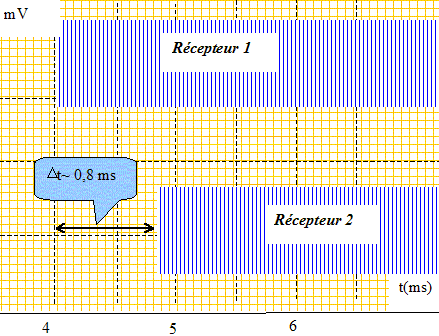Afin de déterminer la célérité des ondes ultrasonores, on réalise une acquisition (sur une durée inférieure à celle d'une salve) pour une distance d = 0,3 m donnant les enregistrements ci-dessous : Indiquer sur la figure le retard Dt correspondant et le mesurer. En déduire la valeur V1 de la célérité des ondes ultrasonores dans l'air. V1 = d/Dt = 0,3/ 8 10-4 =375 m/s ~ 4 102 m/s. Obtiendrait-on le même résultat pour la célérité si on effectuait l'expérience en utilisant l'eau à la place de l'air comme milieu de propagation? Justifier.  La célérité dépend du milieu de propagation : dans l'eau la célérité des ultrasons sera donc différente.   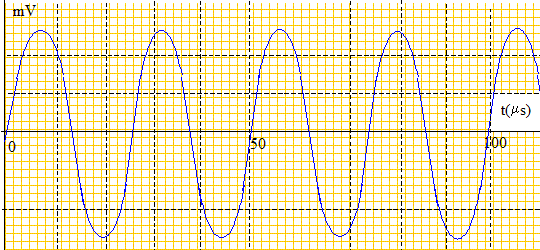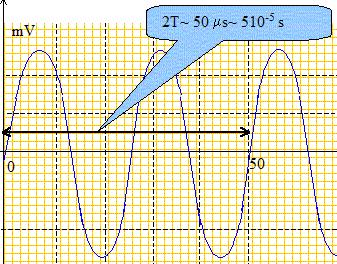Détermination de la célérité des ultrasons : 2ème méthode. On fait maintenant fonctionner l'émetteur en mode " Continu ". On visualise cette fois-ci les signaux à l'aide d'un oscilloscope : le récepteur A est relié à la voie 1 et le récepteur B à la voie 2. Au départ, on place à nouveau les deux récepteurs en face de l'émetteur, côte à côte, comme sur le schéma simplifié du montage de départ. Les deux signaux sont alors superposés et confondus. En choisissant une sensibilité verticale de 0,10 V/div et une sensibilité horizontale de 10 µs/div on obtient l'oscillogramme du signal capté par le récepteur A ci-dessous : Déterminer la période et en déduire la fréquence des ultrasons. période T = 2,5 10-5 s. fréquence(Hz) = 1/ période (s) f = 1/ 2,5 10-5 = 4,0 104 Hz = 40 kHz On déplace le récepteur B en l'éloignant du récepteur A, ce dernier étant fixé. Le déplacement s'effectue dans la direction émetteur-récepteur selon un axe parallèle à l'axe x'x du schéma simplifié du montage : les deux sinusoïdes se décalent puis se superposent à nouveau. On répète l'opération d'éloignement du récepteur B jusqu'à la 10ème superposition des courbes. La distance d1 entre A et B est alors de 8,4 cm. Utiliser ces données pour déterminer la valeur d'une grandeur caractéristique de l'onde que l'on nommera. A chaque nouvelle superposition, le récepteur B s'est déplacé d'une longueur d'onde par rapport à A fixe. longueur d'onde l = d1/10 = 8,4/10 = 0,84 cm = 8,4 10-3 m. Déterminer une valeur V2 de la célérité des ultrasons. célérité ( m/s )= longueur d'onde ( m) * fréquence (Hz). V2 = l f V2= 8,4 10-3* 4,0 104 = 3,4 102 m s-1. 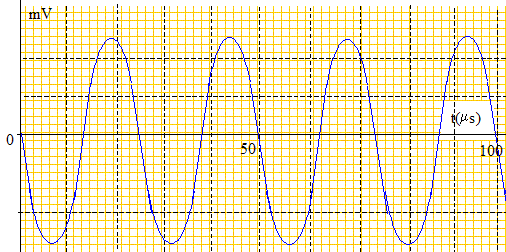On donne ci-dessous le signal capté par le récepteur B lorsqu'il a été décalé d'une autre distance d2 par rapport au récepteur A. On néglige tout amortissement. La distance d2 étant comprise entre 3,5 cm et 4,0 cm, déduire la valeur de d2.   Le signal reçu par le récepteur 2 est en opposition de phase avec le signal reçu par le récepteur 1. La distance d2 des deux récepteurs est un multiple impair de la demi longueur d'onde l. d2 = (2n+1)l/2 = (2n+1)*0,42 cm. De plus d2 est compris entre 3,5 et 4,0 cm d'où : 3,5/0,42 = 8,3 ; 4/0,42 = 9,5 : (2n+1) est entier et égal à 9 Par suite d2 = 9*0,42 = 3,78 cm ~ 3,8 cm. Détection de distance. Une voiture est équipée d'un système comportant un émetteur et un récepteur d'ultrasons placés côte à côte à l'arrière du véhicule. Lors d'une marche arrière, une salve ultrasonore est envoyée et réfléchie par un obstacle puis détectée par le récepteur Dt= 9,0 ms après l'émission, la célérité du son étant considérée comme égale à 1,2.103 km.h-1. À quelle distance se trouve l'obstacle de la voiture? Justifier la réponse. distance aller + distance retour = célérité (m/s) * Dt(s) célérité : 1,2 103/3,6 =333,3 m/s ; Dt = 9,0 10-3 s ; distance aller + distance retour = 333,3 * 9,0 10-3 = 3 m distance obstacle- voiture = 1,5 m.

retour -menu