Méthode d'Euler

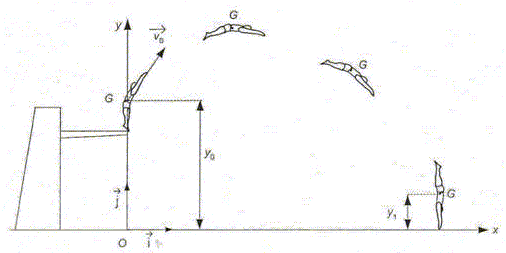
On se propose d'étudier dans un premier temps, le mouvement du centre d'inertie G d'un plongeur de masse m= 70,0 kg lors de son saut et dans une deuxième partie, son évolution dans l'eau. Le mouvement du centre d'inertie du plongeur est étudié dans le repère d'axes (Ox, Oy). Le point O est au niveau de la surface de l'eau et l'altitude du centre d'inertie G du plongeur est notée y. On prendra g = 9,80 m/s2 et on considérera le référentiel galiléen. Etude du saut. Dans toute cette partie on néglige l'action de l'air sur le plongeur au cours de son mouvement et on admet que lors du saut, les mouvements de rotation du plongeur ne perturbent pas le mouvement de son centre d'inertie. On note y0 l'ordonnée du centre d'inertie du plongeur juste avant le saut et v0 sa vitesse initiale. y0 = 4,0 m et v0 = 4,0 m/s.   Une méthode de résolution numérique possible, la méthode d'Euler permet de calculer de façon approchée la valeur algébrique de la vitesse instantanée verticale vy à différentes dates. On note vy(tn) la valeur algébrique de la vitesse instantanée à la date tn ; on note vy(tn+1) la valeur algébrique de la vitesse instantanée à la date tn+1 =tn +Dt. vy(tn+1) = vy(tn) + ay (tn)Dt. (1) ay : composante verticale de l'accélération ; Dt =1,20 10-2 s est le pas de calcul. Compte tenu des valeurs numériques, l'équation différentielle permet d'obtenir la relation suivante : ay(t)=2,14 vy2(t)-0,700. (2) Compléter le tableau suivant : date en s vy en m/s ay en m/s2 tn = 1,44 10-1 vy(tn) = -2,21 ay(tn)= 9,75 tn+1 = 1,56 10-1 vy(tn+1) = -2,09 ay(tn+1)=8,67 tn+2 = 1,68 10-1 vy(tn+2)=-1,99 ay(tn+2)=7,77 (1) conduit à : vy(tn+1) =-2,21 + 9,75 *1,2 10-2 = -2,09. (2) conduit à : ay(tn+1) =2,14*(-2,09)2 -0,700 = 8,67.   Web www.chimix.com Circuit RL II. Circuit RL : on remplace la pile maison par un générateur de tension stabilisée de fem E=1,5 V. Le montage électrique consiste en une association série d'une bobine réelle (L ; r= 8,6 W), d'un conducteur ohmique (R=10 W ), d'un interrupteur et du générateur. 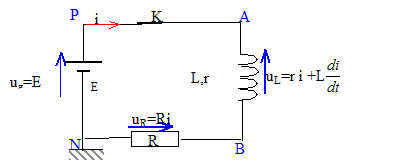Méthode numérique d'Euler : - Etablir l'équation différentielle traduisant l'évolution temporelle du courant i(t). - La méthode d'Euler introduit les notations suivantes : di/dt = Di/Dt pour D t petit. i(tn+1) =i(tn) + Di(tn) avec tn+1 = tn + Dt ( pas de résolution). Recopier et compléter le tableau suivant : t i di/dt s A As-1 0 0 36,59 5,00 10-4 0,018 28,29 1,00 10-3 1,50 10-3 2,00 10-3 2,50 10-3 0,058 10,11 3,00 10-3 0,063 7,82 Quels est l'intérêt et l'inconvénient du choix d'un pas de résolution inférieur à 5 10-4 s ?   équation différentielle traduisant l'évolution temporelle du courant i(t) : ug = uL+uR ; E= ri+Ldi/dt+Ri Ldi/dt + (R+r)i = E soit di/dt = E/L-(R+r)/L i = E/L-454 i= 36,59-454 i compléter le tableau : i(10-3) =i(5 10-4) + Di(tn) = i(5 10-4) + (di/dt)5 10-4Dt = 0,018+28,29*5 10-4 = 0,0321 A (di/dt) 10-3=36,59-454 *0,0321=21,99. i(1,5 10-3) =i(1 10-3) + Di(tn) = i(1 10-3) + (di/dt) 10-3Dt = 0,0321+21,99*5 10-4 = 0,0431 A (di/dt) 1,5 10-3=36,59-454 *0,0431=17,02. i(2 10-3) =i(1,5 10-3) + Di(tn) = i(1,5 10-3) + (di/dt) 1,5 10-3Dt = 0,0431+17,02*5 10-4 = 0,0516 A (di/dt) 1,5 10-3=36,59-454 *0,0516=13,16.   t i di/dt s A As-1 0 0 36,59 5,00 10-4 0,018 28,29 1,00 10-3 0,032 21,99 1,50 10-3 0,043 17,02 2,00 10-3 0,052 13,16 2,50 10-3 0,058 10,11 3,00 10-3 0,063 7,82 avec un pas plus petit on augmente la précision, mais on multiplie le nombre de calculs.

retour -menu