Aurélie 14/06/07
 

cinétique, conductivité, 2-chloro-2-méthylpropane bac S 2007 Afrique

 http://www.edulyautey.org/~physique/

Google

Le 2-chloro-2-méthylpropane réagit sur l'eau pour donner naissance à un alcool. Cet alcool est le 2-méthylpropan-2-ol. La réaction est lente et totale.

On peut modéliser cette transformation par :

(CH3)3C-Cl+2H2O =(CH3)3C-OH + H3O+ + Cl-.

Masse molaire du 2-chloro-2-méthylpropane : M= 92,0 g/mol ; masse volumique: r= 0,85 g/mL

Conductivités molaires ioniques en S m2 mol-1 : lH30+=349,8.10-4 ; lCl-= =76,3.10-4.

Protocole observé:

Dans une fiole jaugée, on introduit 1,0 mL de 2-chloro-2-méthylpropane et de l'acétone afin d'obtenir un volume de 25,0 mL d'une solution S. Dans un bécher, on place 200,0 mL d'eau distillée dans laquelle est immergée la sonde d'un conductimètre. Puis à l'instant t = 0 min, on déclenche un chronomètre en versant 5,0 ml de la solution S dans le bêcher. Un agitateur magnétique permet d'homogénéiser la solution obtenue, on relève la valeur de la conductivité du mélange au cours du temps.

  1. Montrer que la quantité initiale de 2-chloro-2-méthylpropane introduite dans le dernier mélange est n0 = 1,8.10-3mol.
  2. Etablir le tableau d'avancement. Quelle relation lie [H3O+] et [Cl-] à chaque instant ?
  3. Donner l'expression de la conductivité s du mélange en fonction de [H3O+] et des conductivités molaires ioniques.
  4. Donner l'expression de la conductivité s du mélange en fonction de l'avancement x de la réaction, du volume V du mélange réactionnel et des conductivités molaires ioniques des ions présents dans la solution.
  5. Pour un temps très grand, la conductivité notée s00 du mélange ne varie plus. Sachant que s00 = 0,374 S.m-1,vérifier que la transformation envisagée est bien totale.
  6. Exprimer le rapport s /s00. En déduire l'expression de l'avancement x en fonction de s, s00 et de l'avancement maximal xmax de la réaction.
  7. Pour s = 0,200 S.m-1, quelle est la valeur de x ?
Quantité initiale de 2-chloro-2-méthylpropane introduite dans le dernier mélange :

masse (g) = volume (mL)*masse volumique (g/mL)

m =V r= 1,0*0,85 = 0,85 g.

Quantité de matière (mol) = masse (g) / masse molaire (g/mol)

n = m/M = 0,85 / 92,0 = 9,24 10-3 mol dans 25 mL

soit n0 = 9,24 10-3 /5 ; n0 = 1,8 10-3 mol dans 5 mL.

Tableau d'avancement :
avancement (mol)
(CH3)3C-Cl
+2H2O
= (CH3)3C-OH
+ H3O+
+ Cl-
initial
0
n0
excès
0
0
0
en cours
x
n0 -x
x
x
x
final
xmax
n0-xmax
xmax
xmax
xmax
[H3O+] = [Cl-] = x/V.

 

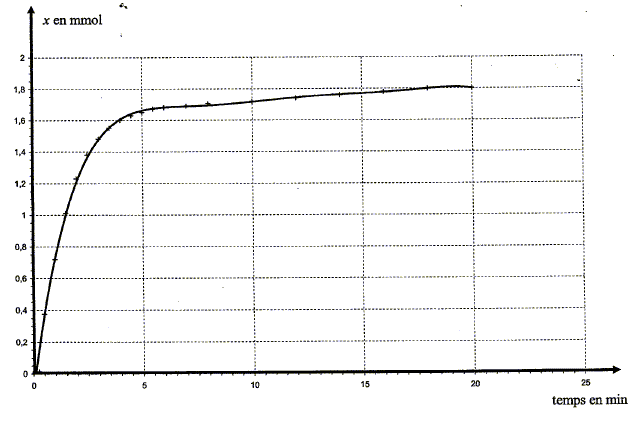
Expression de la conductivité s du mélange en fonction de [H3O+] et des conductivités molaires ioniques :

s =lH30+[H3O+] +lCl- [Cl-] ; s = (lH30+ + lCl- ) [H3O+] avec [H3O+] en mol m-3.

s = (lH30+ + lCl- ) x/V avec V en mol m3.

Vérifions que la transformation envisagée est bien totale :

Pour un temps très grand, la conductivité notée s00 du mélange ne varie plus.

s00 = 0,374 S.m-1, lH30+=349,8.10-4 ; lCl- =76,3.10-4 S.I, V = 205 mL =2,05 10-4 m3.

x00= s00 V / (lH30+ + lCl- )

x00=0,374*2,05 10-4 /((349,8 + 76,3)10-4 ) =1,8 10-3 mol.

On constate que x00= xmax = n0 : la transformation est totale.

Expression du rapport s /s00 :

s = (lH30+ + lCl- ) x/V ; s00 = (lH30+ + lCl- ) xmax/V ; s /s00 = x/xmax.

Expression de l'avancement x en fonction de s, s00 et de l'avancement maximal xmax de la réaction.

x= xmax s /s00

Pour s = 0,200 S.m-1, la valeur de x est égale à :

x= 1,8 10-3 *0,200 / 0,374 = 9,6 10-4 mol.

Exploitation des résultats

L'expression établie permet de construire la courbe montrant les variations de l'avancement x de la réaction en fonction du temps.

La vitesse volumique v de réaction est donnée par la relation: v =1/V dx/dt où Vest le volume de la solution et x l'avancement de la réaction.

  1. Expliquer la méthode qui permettrait d'évaluer graphiquement cette vitesse à un instant donné.
  2. À l'aide de la courbe, indiquer comment évolue cette vitesse au cours du temps.
  3. Quel facteur cinétique permet de justifier cette évolution ?
  4. Définir le temps de demi-réaction et estimer graphiquement sa valeur.
  5. On réalise maintenant la même expérience à une température plus élevée.
    - Dessiner qualitativement sur le graphique l'allure de la courbe montrant les variations de l'avancement x au cours du temps.
    - La valeur du temps de demi-réaction est-elle identique, inférieure ou supérieure à la valeur précédente? Justifier.
 

 

Méthode permettant d'évaluer graphiquement cette vitesse à un instant donné :

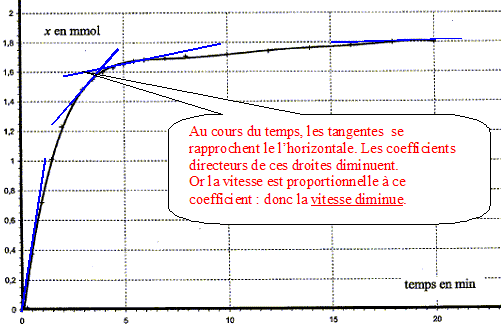
A la date t considérée, tracer la tangente à la courbe x=f(t)

Déterminer graphiquement le coefficient directeur [dx/dt]t de cette droite tangente.

Diviser ce coefficient par le volume V ( en litre) de la solution.

A l'aide de la courbe, indiquer comment évolue cette vitesse au cours du temps.

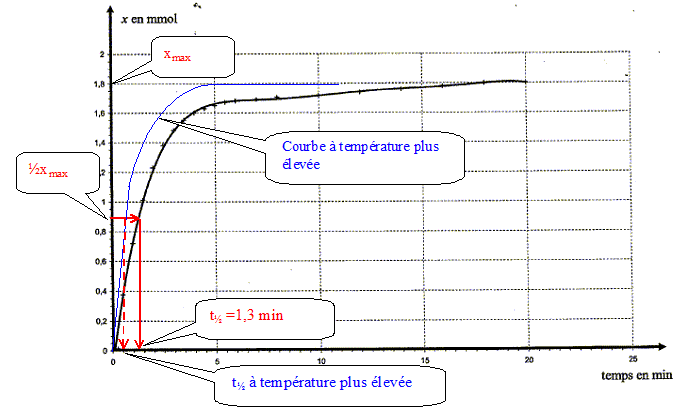
Le facteur cinétique permettant de justifier de cette évolution est la concentration du réactif :

au cours du temps celle-ci diminue et en conséquence la vitesse diminue.

Temps de demi-réaction et estimation graphique de sa valeur :

Durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final.

Ici xfin = xmax = 1,8 10-3 mol donc xt½ = ½xmax= 9,0 10-4 mol.

La température est un facteur cinétique : à température plus élevée la vitesse augmente : la composition finale est plus rapidement atteinte et le temps de demi réaction diminue.

 
 
retour -menu