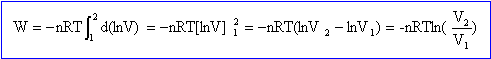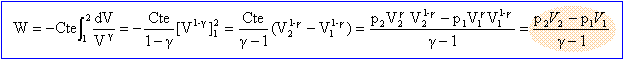gaz parfait : isotherme, adiabatique, isochore, travail, entropie

Une enceinte cylindrique fermée par un piston, mobile sans frotement, contient 500 g d'hélium gazeux, monoatomique, de masse molaire M=4 g/mol. Dans l'état (1) initial, le volume de l'enceinte est V1= 100 littres, et le gaz,supposé parfait, est à la température T1=600 K.On rappelle que l'énergie interne de n mole de gaz parfait monoatomique à la température T s'écrit U=3/2nRT où R=8,31 J mol-1 K-1. R désigne la constante des gaz parfaits. Capacité thermique massique à volume constant Cv de l'Hélium (en kJ K-1 kg-1). Cv = 1,5R = 1,5*8,31 =12,46 J K-1 mol-1 ; Cv =12,46 / 0,004 J K-1 kg-1 = 3116 J K-1 kg-1 = 3,12 kJ K-1 kg-1. Par déplacement du piston, le gaz subit une détente isotherme, supposée réversible, qui le conduit à la l'état (2) caractérisé par un volume V2=250 littres. Calcul de la pression P2 du gaz dans l'état (2). P1V1 = nRT1 ; n = 500/4 = 125 mol ; V1 = 0,1 m3. P1= nRT1 /V1 = 125*8,31*600/0,1 = 6,23 106 Pa. P1V1 = P2V2 ; P2 = P1V1 /V2 =6,23 106 *0,1 / 0,25 =2,50 106 Pa. Travail W1,2 reçu par ce gaz au cours de cette évolution isotherme.   travail élémentaire des forces de pression -pdV= -nRT /V dV = -nRT d(lnV) intégrer entre v1 et v2. avec nRT=p1v1 = p2v2 = 6,23 106 *0,1 = 6,23 105 ; v2 /v1 = 250/100 = 2,5 W = -6,23 105 ln 2,5 = -5,71 105 J On envisage une nouvelle évolution réversible, constituée d'une détente adiabatique entre l'état (1) et un état intermédiaire (3) de volume V2=V3, suivie d'un chauffage isochore entre l'état (3) et l'état final (2), défini précédemment. Température T3 l'état intermédiaire. PVg = cste et P = nRT/V d'où Vg-1T = cste V1g-1 T1 =V3g-1 T3 = =V2g-1 T3 ; T3 = T1 (V1/V2)g-1 T avec g = 1,67 T3 = 600 (100/250)0,67 = 326 K. Calculer le travail W reçu par le gaz au cours des évolutions successives. adiabatique 1-->3 : travail élémentaire des forces de pression -pdV avec p= Cte / Vg intégrer entre V1 et V2. soit dans ce cas : W13 = (p3V3-p1V1) / (g-1) = nR(T3-T1) /(g-1) W13 =125*8,31(326-600)/0,67 = -4,27 105 J. Autre méthode : adiabatique donc Q13=0, par suite DU13 = W13+Q13 = W13. DU13 =1,5 n R((T3-T1) = 1,5*125*8,31*(-276) = -4,3 105 J. Le travail des forces de pression est nul au cours d'une transformation isochore. Variation d'entropie du gaz entre l'état (1) et l'état (2).   L'entropie est une fonction d'état ; sa variation ne dépend que des états initial et final, pas du chemin suivi. La transformation (1) -->(2) isotherme est réversible. transformation élémentaire : dS =dQ/T= (dU-dW)/T =nCv /T dT+ PdV/T = nR/(g-1) /T dT+ nRdV/V intégrer entre l'état 1 et l'état 2 : DS =nCv ln(T2 /T1) + nRln(V2/V1) = nRln(V2/V1). DS = 125*8,31 ln(250/100) = 951 J K-1. De l’air considéré comme gaz parfait subit une détente de 10 atm à 1 atm à la température de 25°C. Calculer le travail fourni par le gaz si : a) La détente est effectuée de manière réversible : La pression extérieure est toujours égale à la pression du gaz : dW = -Pext dV avec P = nRT/V ; dW = - nRT dV/V= -nRT d(ln V). Intégrer entre l'état 2 ( final) et l'état 1 ( initial ) : Wrév = -nRT ln (V2/V1) = -nRT ln (P1/P2) Pour n = 1 mole : Wrév = -8,31*298 ln(10) = -5,7 103 kJ mol-1. b) La détente est effectuée de manière irréversible. Wirrév = -P( V2-V1) = nRT(V1/V2-1) = nRT(P2/P1-1) Pour n = 1 mole : Wirrév = 8,31*298 (0,1-1) = -2,2 103 kJ mol-1. Cette valeur est inférieure à celle du cas réversible. On considère un gaz parfait dans la condition initiales (PA=3 atm, TA=300 K, VA=16,4 L) auquel on fait subir de transformations réversibles suivantes : ( on donne g = 1,66) Etat A --> Etat B ; compression adiabatique jusqu’ à TB=450 K. État B --> Etat C : refroidissement isochore jusqu’à PC=4,05 atm. État --> Etat D : détente isotherme jusqu’ à PD=3 atm. État D --> Etat A : isobare. Déterminer les variable d’état (P, V, T) de chaque étape. A-->B : adiabatique réversible P1-g Tg = Cste ; PA1-g TAg =PB1-g TBg ; PB = PA (TA / TB)g /(1-g) = 3(300/450)-2,52 ; PB = 8,3 atm. Loi des gaz parfaits : VB = VA PA TB/( PB TA) = 16,4 *3*450/(8,3*300) ; VB = 8,9 L. B-->C : ioschore réversible VC= 8,9 L. Loi des gaz parfaits : TC = TB PC / PB = 450*4,05/8,3 ; TC =220 K. C-->D : iotherme réversible TD= 220 K. Loi des gaz parfaits : VD = VC PC / PD = 8,9*4,05/3 ; VD =12 L. Représenter les différentes transformations sur un diagramme de Clapeyron. Calculer le travail, la chaleur, la variation d’énergie interne et d’enthalpie, pour chacune des transformations. 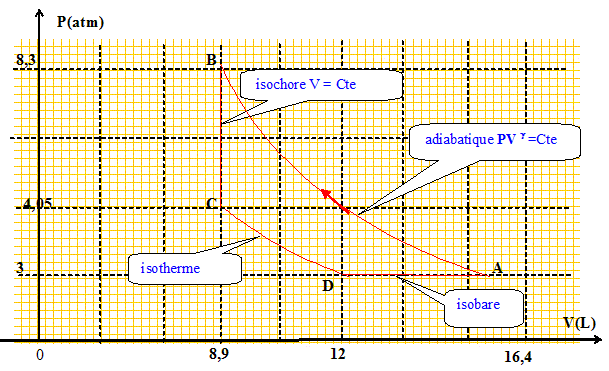A-->B : adiabatique réversible QAB=0 ; WAB=( 8,3 105*8,9 10-3 - 3 105*16,4 10-3 ) / 0,66 ; WAB= 3,74 kJ ; DUAB= 3,74 kJ ; DHAB= n Rg/(g-1)DT=2*8,31*1,66/0,66 *150 ; DHAB= 6,3 kJ. B-->C : isoschore réversible WBC=0 ; QBC= DUBC= n R/(g-1)DT ; n = PAVA/(RTA) =3 105 * 16,4 10-3 /(8,31*300) ~2 mol. QBC=2*8,31/0,66 *(220-450) ; QBC= -5,8 kJ. DUBC= -5,8 kJ ; DHBC= n Rg/(g-1)DT=2*8,31*1,66/0,66 *(220-450) ; DHBC= -9,6 kJ. C-->D : isotherme réversible DUCD=0 ; DHCD=0 ; QCD= -WCD=nRT ln (VD/VC) = nRT ln (PC/PD) QCD= 2*8,31*220 ln(12/8,9) ; QCD= 1,1 kJ ; WCD= -1,1 kJ C-->D : isobare réversible. DHCD= n Rg/(g-1)DT=2*8,31*1,66/0,66 *(300-220) ; DHBC= 3,3 kJ. DUCD= n R/(g-1)DT=2*8,31/0,66 *(300-220) ; DHBC= 2,0 kJ. WDC=P(VD-VC) =3 105(16,4 10-3-12 10-3) ; WDC= 1,3 kJ ; QDC= DUCD= - WDC= 2,0-1,3 ; QDC=0,7 kJ. Montrer que le premier principe est vérifié. DUcycle=0 ; DHcycle=0 ; Somme de travaux Wtotal = 3,7-1,1+1,3 ~3,9 kJ Somme des quantités de chaleur Qtotal = -5,8+1,1+0,7 ~ -4 kJ ; Wtotal +Qtotal ~0.

retour -menu