interaction de fluorescence, atténuation par le plomb d'après IMRT

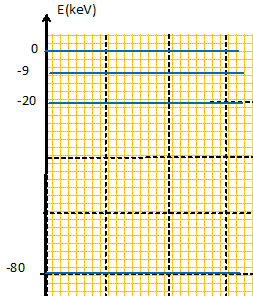
Interaction de fluorescence : Les énergies des électrons des couches K, L et M du platine ont pour valeurs : EK= -80 keV ; EL= - 20 keV ; EM = -9 keV. Représenter le diagramme énergétique de ces électrons.   Un électron incident ionise un atome de platine de l'anti-cathode en lui arrachant un de ses électrons K. Calculer l'énergie cinétique ECS ( eV et J) et la vitesse v de cet électron secondaire émis. On suppose le choc parfaitement élastique et l'électron non relativiste. U = 90 kV ; me =9,1 10-31 kg. Energie de l'électron incident : 90 keV ; énergie ( valeur absolue) des électrons de la couche K  : 80 keV d'où ECS = 90-80 = 10 keV ; 10*103*1,6 10-19 =1,6 10-15 J. ½mev2 = ECS ; v = [2 EC / me]½ = [3,2 10-15 / 9,1 10-31 ]½ =5,9 107 m/s. L'ionisation précédente est suivie d'un phénomène de fluorescence ; calculer la longueur d'onde l de la raie spectrale émise lorsque l'atome ionisé revient dans son état fondamental. L'atome ionisé capture un électron du milieu extérieur ; un photon d'énergie 80 keV est émis. 80 keV = 80 103*1,6 10-19 J = 1,28 10-14 J. l = hc/E = 6,63 10-34*3 108/ 1,28 10-14 =1,55 10-11 m. Au lieu de revenir dans son état fondamental, l'atome ionisé subit un réarrangement électronique ; quel nom donne t-on à ce phénomène ? fluorescence. Calculer la longueur d'onde du photon émis au cours de la transition d'un électron de la couche M à la couche L. E = EM-EL =-9 +20 = 11 keV = 11 103*1,6 10-19 J =1,76 10-15 J. l = hc/E = 6,63 10-34*3 108/ 1,76 10-15 =1,13 10-10 m. 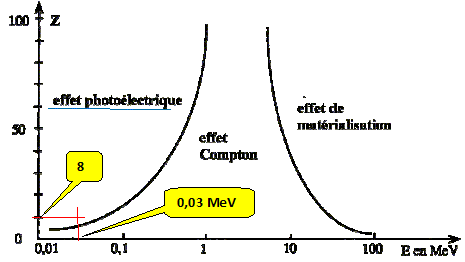Pénétration du rayonnement dans la matière : On considère des photons d'énergie 30 keV émis par le tube, se propageant dans les tissus que l'on considérera en première approximation comme constitués d'eau de numéro atomique moyen égal à 8 et dont la masse volumique est 1 g cm-3. A l'aide du diagramme ci-dessous déterminer le type d'interaction que ce type de photons présente avec les tissus traversés.   Le coefficient massique d'atténuation dans l'eau est 0,45 cm2 g-1 pour ce type de photons. 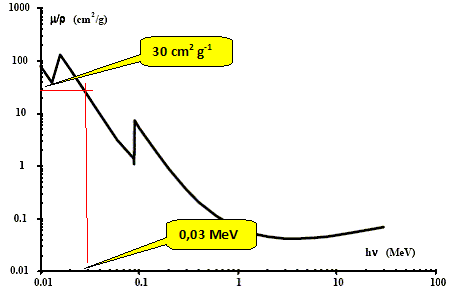Calculer le coefficient d'atténuation linéique correspondant. coef d'atténuation linéïque ( cm-1)= coef d'atténuation massique (cm2 g-1)* masse volumique( g cm-3). d'où m = 0,45*1 = 0,45 cm-1. Calculer la couche de demi-atténuation dans l'eau. CDA : épaisseur de matériau ( mètre) atténuant d'un facteur 2 le nombre initial de photons ( ou division par deux de l'énergie des photons initiaux ) m . CDA = ln 2. CDA = ln2 / 0,45 =1,5 cm. Le graphe ci-dessous en coordonnées logarithmiques, donne l'évolution du coefficient massique d'atténuation pour le plomb. la masse volumique du plomb vaut 11340 kg m-3. Déterminer graphiquement le coefficient massique d'atténuation du plomb pour des photons de 30 keV. En déduire le coefficient d'atténuation linéique correspondant. coef d'atténuation linéïque ( cm-1)= coef d'atténuation massique (cm2 g-1)* masse volumique( g cm-3). 11340 kg m-3 = 11,34 g cm-3 ; d'où m = 30*11,34 = 340 cm-1. Calculer l'épaisseur de la couche de décitransmission ( l'intensité du faisceau est divisée par 10) pour le plomb, pour ces photons. CDT : l'intensité du faisceau est divisée par 10 : m . CDT = ln 10. CDT = ln10 / 340 = 6,8 10-3 cm. En déduire l'épaisseur de plomb nécessaire à la réduction de l'intensité du faisceau ( pour ces photons) au millième de sa valeur. 0,001 = exp (-m . LPb ) ; m . LPb = ln 1000 ; LPb =ln1000 / 340 =2,0 10-2 cm.

retour -menu