|
Rayons X, Tube de Coolidge, atténuation d'après IMRT 08 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
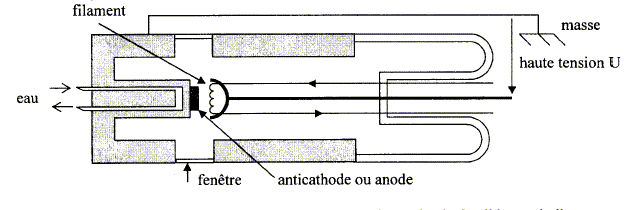
Un tube à rayons X est constitué d'une cathode émettrice d'électrons et d'une anode en tungstène. On applique entre la cathode C et l'anode A une tension accélératrice qui peur varier entre 50 kV et 100 kV. Tube de Coolidge : tube dans lequel règne un vide poussé (environ 10-4 Pa). Les électrons sont émis par un filament de tungstène chauffé par un courant électrique (effet Joule). Le filament joue le rôle de cathode. On établit entre la cathode et l'anode une tension élevée ; celle-ci accélère les électrons émis par le filament. Les électrons accélérés frappent l'anode. La plus grande partie de la puissance électrique (99 %) est dissipée sous forme de chaleur dans l'anode. Les tubes sont refroidits par une circulation d'eau.
Signe de la tension accélératrice UAC appliquée entre les deux électrodes : La vitesse initiale des électrons est négligeable ; le poids des électrons est négligeable devant la force électrique. La seule force qui travaille est la force électrique : son travail est moteur et vaut W= eUAC ( e : charge élémentaire positive) UAC est donc positive. Expression de l'énergie cinétique des électrons arrivant sur l'anode : Les électrons sont émis au niveau de la cathode avec une énergie cinétique d'une dizaine d'électrons-volts. Le théorème de l'énergie cinétique s'écrit : Ec finale - Ec départ = eUAC. UAC étant de l'ordre de 50 à 100 keV, eUAC est de l'ordre de 50 à 100 keV. Cette valeur est très supérieure à l'énergie cinétique initiale des électrons. En conséquence Ec départ peut être négligée devant eUAC et Ec finale = eUAC.
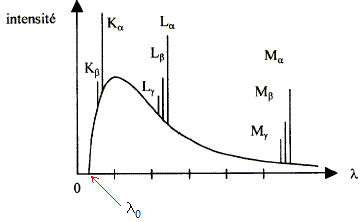
Le spectre d'émission est formé
d'un fond continu sur lequel se superposent des
raies d'émission intenses. On admet que certains électrons sont
arrêtés brutalement dans
l'anticathode. énergie du rayonnement X : E= hc/l0
= eU d'où l0
= hc/(eU) = k/U avec k = hc/e
On admet que l'énergie des photons les plus nombreux vaut environ les 2/3 de l'énergie maximale de ceux-ci.
Définir le courant anodique et calculer son intensité. En déduire le nombre d'électrons se déplaçant de la cathode vers l'anode en 1 s. Entre anode et cathode règne un vide poussé. Le déplacement des électrons entre ces deux électrodes correspond au courant anodique. L'intensité I de ce courant est égale à la puissance divisée par la tension U : I= P/U =1500/105 =1,5 10-2 A. Quantité d'électricité correspondante : Q = I t avec t = 1 s ; Q = 1,5 10-2 C. La charge, en valeur absolue, d'une mole d'électrons vaut 96500 C. Quantité de matière d'électrons (mol) n = 1,5 10-2 / 96500 =1,55 10-7 mol Dans une mole d'électron il y a NA = 6,02 1023 électrons, d'où :1,55 10-7 *6,02 1023 =9,4 1016 électrons. Puissance émise par le tube sous forme de rayonnement : La plus grande partie de la puissance électrique (98 %) est dissipée sous forme de chaleur dans l'anode. Puissance émise sous forme de rayonnement : 1500*0,02 = 30 W. En supposant que tous les photons émis par le tube ont une énergie moyenne de 60 keV, le nombre N de photons émis en une seconde est : 60 keV = 6 104 *1,6 10-19 J =9,6 10-15 J ; 30 W = 30 J s-1. N = 30/9,6 10-15 =3,1 1015 photons. ( c'est à dire 3,3 % du nombre d'électrons du courant anodique) Si la tension
accélératrice est divisée par deux ( 50
keV), le rendement est divisé par deux.
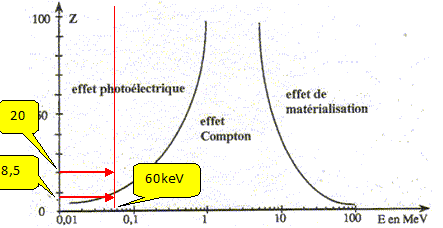
En utilisant le graphe ci-après, déterminer le type d'interaction que ce type de photons présente avec la chair ( numéro atomique moyen 8,5) et l'os ( numéro atomique moyen 20). Donner une brève description des trois types d'interaction évoquées sur le graphique. Effet photoélectrique : Lorsqu'un photon X, assez énergétique, arrive à proximité d'un électron d'une couche profonde, le photon est absorbé et un électron est éjecté : ce dernier emporte de l'énergie sous forme cinétique. La probabilité d'interaction par un effet photoélectrique est proportionnelle au cube du numéro atomique des atomes constituants le milieu. Un électron d'une couche superficielle vient prendre la place de l'électron éjecté : un photon de faible énergie (pour les atomes constitutifs des matières organiques) est émis. Effet Compton : Lorsqu'un photon X passe à proximité d'un électron périphérique peu lié à l'atome, l'énergie du photon est en partie transmise à l'électron : ce dernier est arraché de l'atome et s'échappe avec une certaine énergie cinétique. Le reste de l'énergie se retrouve sous la forme d'un photon X de direction différente et d'énergie inférieure. La probabilité d'interaction par un effet Compton ne dépend pas du numéro atomique. L'effet Compton est prépondérant dans les tissus organiques avec des photons X de grande énergie. Effet de matérialisation : Le photon ( d' énergie supérieure à 1,02 MeV) disparaît : il donne naissance à un électron et à son anti-particule, le positon. Le flux travers une épaisseur de chair de L= 4,0 cm ; le coefficient d'atténuation linéïque du muscle vaut m = 0,213 cm-1. Calculer l'intensité du faisceau émergent. I = I0 exp (-µL) ; I = 0,5 exp(-0,213*4,0) = 0,21 W m-2. Le coefficient d'atténuation linéïque de l'os, pour ces mêmes photons, vaut m = 0,519 cm-1. Calculer l'intensité du faisceau émergent lorsqu'il a traversé successivement 1,0 cm de chair, puis 2,0 cm d'os, puis à nouveau 1,0 cm de chair. Conclure. Après traversée de 1 cm de chair, l'intensité du faisceau émergent vaut : I1 = 0,5 exp(-0,213*1,0) = 0,40 W m-2. Après traversée de 2 cm de chair, l'intensité du faisceau émergent vaut : I2 = 0,40 exp(-0,519*2,0) = 0,14 W m-2. Après traversée de 1 cm de chair, l'intensité du faisceau émergent vaut : I3 = 0,14 exp(-0,213*1,0) = 0,11 W m-2. ou encore additionner les produits µL = 0,213*1,0 + 0,519*2,0 +0,213*1,0 = 1,464. Puis I= 0,5 exp(-1,464) = 0,116 W m-2. ( atténuation du faisceau initial : 55 %)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|