|
Autour du Cobalt 60 d'après IMRT |
||||||
|
||||||
|
Pour l'atome de cobalt 60 on donne les renseignements suivants : Z=27 ; A = 58 ; M= 58,933 g/mol. Donner le nom et la signification des symboles Z, A, M. Z : numéro atomique, nombre de charge, nombre de protons ( 27) A : nombre de nucléons ou nombre de masse ; 58 nucléons soit 58-27 = 31 neutrons. M : masse atomique molaire. Donner les 4 nombres quantiques qui définissent un état électronique. Préciser leur nom et les relations qui existent entre ces nombres. n : nombre quantique principal ( n= 1, 2, 3, 4, 5 ,6 ...) l : nombre quantique secondaire : l prend les valeurs entières 0, 1, 2, .... n-1. m : nombre quantique magnétique ; il prend les valeurs entières comprises entre -l et +l. s : nombre de spin : deux valeurs possibles +½ et -½. Donner les nombres quantiques caractérisant les états électroniques 4s, 3d, 4f. 4s : n=4 ; l =0, m=0 , s=+½ ou -½. 3d : n=3 ; l=2 ; m : -2 ; -1 ; 0 ; 1 ; 2 ; s=+½ ou -½. 4f : n=4 ; l =3 ; m : -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; s=+½ ou -½. Décrire la structure du nuage électronique de l'atome de cobalt. 1s2 2s2 2p6 3s2 3p6 4s2 3d7. Le spectre d'émission d'une lampe à vapeur de sodium montre des raies à : l1 = 568,8 nm ; l2 = 589,3 nm ; l3 = 615,4 nm ; l4 = 819,5 nm. Le diagramme d'énergie comporte les niveaux
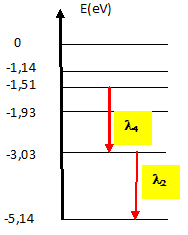
suivants : -5,14 eV( fondamental) ; -3,03 eV ; -1,93 eV ;
-1,51 eV ; -1,18 eV. DE
= hc/ l. DE = hc/
l2
= 6,62 10-34*3 108 / 589,3
10-9 = 3,37 10-19 J 3,37 10-19 /1,6 10-19 =2,1
eV 2,1 est la différence d'énergie
entre le premier état excité et le
niveau fondamental DE = hc/
l4
= 6,62 10-34*3 108 / 819,5
10-9 = 2,42 10-19 J 2,42 10-19 /1,6 10-19
=1,51 eV 1,51 est la différence d'énergie
entre le 3è état
excité et le 1er état
excité
Le cobalt 60 est obtenu par irradiation neutronique dans les réacteurs nucléaires du cobalt 59, isotope stable du cobalt. Données : masse du proton : 1,0072764668 u = 938,272013 MeV c-2. masse du neutron : 1,0086649160 u = 939,565346 MeV c-2; masse de l'électron : 5,4858 10-4 u = 0,51100 MeV c-2. masse atomique du nickel 60 : 59,930786 u ; masse atomique du cobalt 59 : 58,9331955 u ; masse atomique du cobalt 60 : 59,9338174 u ; 1 u = 1,66 10-27 kg = 931,5 MeV c-2. Calculer la masse des noyaux de cobalt 59 et de cobalt 60. cobalt 59 : 58,9331955 * 1,66 10-27 =9,78 10-26 kg ; cobalt 60 : 59,9338174 * 1,66 10-27 =9,95 10-26 kg ; Calculer les énergies de liaison de ces deux noyaux. Justifier la différence de stabilité qui existe entre ces deux noyaux. cobalt 59 : 27 protons et 59-27 = 32 neutrons |Dm|= 27 mP +32 mN- m(59Co) |Dm|= 27*1,0072764668 +32*1,0086649160 -58,9331955 =0,54055 u 0,54055 *931,5 =503,52 MeV c-2 énergie de liaison par nucléon : 503,52/59 =8,534 MeV/nucléon. cobalt 60 : 27 protons et 60-27 = 33 neutrons |Dm|= 27 mP +33 mN- m(60Co) |Dm|= 27*1,0072764668 +33*1,0086649160 -59,9338174 =0,54856 u 0,54856 *931,5 =510,98 MeV c-2 énergie de liaison par nucléon : 510,98 / 60 =8,516 MeV/nucléon. L'énergie de liaison par nucléon du cobalt 59 est supérieure à l'énergie de liaison par nucléon du cobalt 60 : le cobalt 59 est plus stable que le cobalt 60. Ecrire l'équation de cette réaction nucléaire en indiquant les lois utilisées. Le cobalt 60 est obtenu par irradiation neutronique dans les réacteurs nucléaires du cobalt 59. 5927Co+ 01n ---> 6027Co. Conservation de la charge : 27+0=27 ; conservation du nombre de nucléons : 59+1 = 60. Calculer l'énergie libérée par cette réaction. Commenter la valeur obtenue. |Dm| = m(5927Co) +m( 01n)-m(6027Co) =58,9331955+1,008664916-59,9338174=8,043016 10-3 u 8,043016 10-3 * 931,5 = 7,492 MeV. cela représente la différence entre les énergies de liaison du cobalt 60 et du cobalt 59.
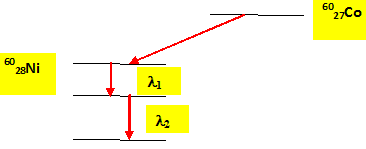
Le cobalt 60 se désintègre par radioactivité bête - pour donner du nickel dans un état excité. Ecrire l'équation de la réaction de désintégration. 6027Co---> 6028Ni + -10e + antineutrino Conservation de la charge : 27 = 28-1 ; conservation du nombre de nucléons : 60 = 60 +0. Chaque année un échantillon de cobalt 60 perd 12,5 % de son activité initiale. Donner l'expression mathématique décrivant l'évolution de l'activité d'une source radioactive en fonction du temps. A(t) = A0 exp(-lt). Déterminer la constante radioactive l du cobalt 60 dans le systéme u.S.I. Au bout d'un an l'activité résiduelle vaut 100-12,5 = 87,5 % de l'activité initiale : 0,875A0 = A0 exp(-l) ; ln 0,875 = -l ; l =0,1335 an-1 =0,1335 / (365*24*3600) s-1 =4,23 10-9 s-1. Calculer la demi-vie ou période du cobalt 60. l t½ = ln2 ; t½ = ln2 /0,1335 = 5,2 ans.
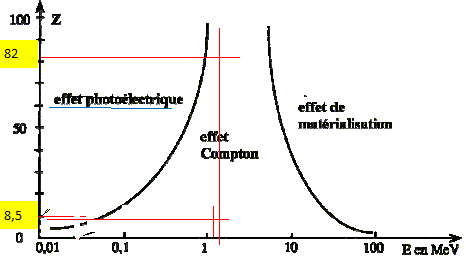
Les photons peuvent se propager dans différents milieux. A l'aide du diagramme donné, déterminer quel(s) type (s) d'interaction(s) ces photons présentent avec l'eau ( Z moyen=8,5) et le plomb (Z=82).
Le traitement d'une tumeur pulmonaire par les photons gamma délivrés par une source de cobalt 60 nécessite un débit dose de 18 gray par heure. Une mesure effectuée dans un fantôme d'eau placé sur le trajet du faisceau gamma émis par la source de cobalt 60 donne un débit dose de 50 gray par heure. Le coefficient linéique d'absorption du plomb est m = 1,15 cm-1. Donner l'expression mathématique décrivant l'évolution du débit de dose D en fonction de l'épaisseur x de plomb traversé. D = D0 exp(-m x). Calculer l'épaisseur de la couche de demi-atténuation (CDA) pour ces photons. m CDA = ln2 ; CDA = ln2 / 1,15 = 0,60 cm. Calculer l'épaisseur du filtre de plomb à interposer sur le trajet du faisceau gamma pour obtenir un débit de dose convenable. 18 = 50 exp(-1,15 x) ; ln(18/50) = -1,15 L ; L = 0,89 cm. Sous l'effet de l'irradiation, les cellules de la tumeur sont détruites et leur nombre évolue selon la loi : N = 2 N0 exp(-½D) où D est la dose absorbée. La tumeur pulmonaire contient environ 1010 cellules. Déterminer la dose nécessaire D si l'on veut réduire cette tumeur à 10 cellules survivantes. 10 = 2 1010 exp(-½D) ; 5 10-10 = exp(-½D) ; ln ( 5 10-10)= -0,5 D ; D = 42,8 gray. Calculer la durée d'exposition si la dose est délivrée en une seule fois. 42,8 / 18 = 2,38 heures.
|
||||||
|
|