|
Radiothérapie métabolique des métastases osseuses d'après DTS IMRT 07 |
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
h = 6,62 10-34 J s ; c= 3,00 108 m/s ; e=1,60 10-19 C ; me = 9,11 10-31 kg = 5,48 10-4 u ; 1 u = 931,5 MeV/c2. Coefficient d'atténuation m de photons d'énergie 103 keV dans le plomb m = 6,93 103 m-1. Energie nécessaire pour former une paire d'ions dans l'eau : w=33 eV.
Radiothérapie métabolique des métastases osseuses. Le principe de la radiographie mtabolique des métastases osseuses repose sur l'utilisation de radioéléments émetteurs béta- à tropisme osseux. Un effet antalgique est obtenu dans 75 % des cas, tandis que leur activité anti-tumorale est possible mais non prouvée. Les différents radioéléments utilisés sont le strontium 89 qui est un émetteur béta- sans gamma et le samarium 153 qui est un émetteur béta - et gamma. Conservation du nombre de nucléons ;
conservation de la charge. Ecrire
l'équation de désintégration
nucléaire du strontium 89 et du samarium
153. 8938Sr--->8939Y+
0-1e + antineutrino 15362Sm
--->15363Eu* +
0-1e + antineutrino 15363Eu*
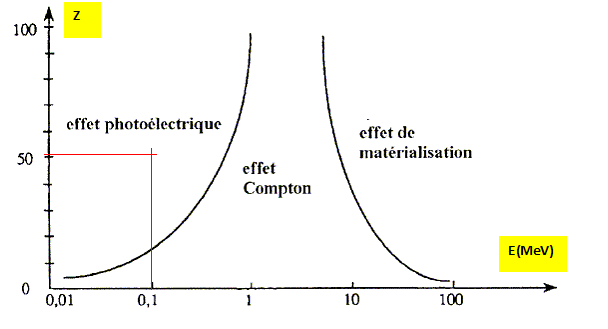
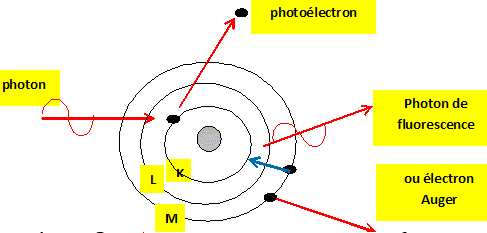
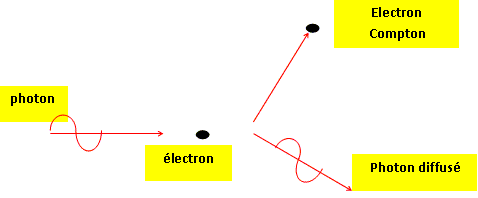
--->15363Eu + gamma. Dm = m(8939Y )+ m( 0-1e)- m (8938Sr) = 88,884 476 + 5,48 10-4 -88,889 606 =- 4,582 10-3 u Energie libérée : 4,582 10-3 *931,5 = 4,268 MeV. Dm = m(15363Eu )+ m( 0-1e)- m (15362Sm) = 152,886 702 + 5,48 10-4 -152,887 604 =- 3,54 10-4 u Energie libérée : 3,54 10-4 *931,5 = 0,3297 MeV. Pour le samarium 153, lors de la désintégration, il y a émmission d'un photon gamma d'énergie E(gamma) = 103 keV. Expliquer le phénomène à l'origine de cette émission. 5363Eu* --->15363Eu + gamma. Désexcitation du noyau fils. Calculer l'énergie cinétique maximale des particules béta- lorsqu'un photon gamma est émis. Conservation de l'énergie : énergie libérée = énergie cinétique de l'électron + énergie emportée par l'antineutrino + énergie du photon gamma énergie libérée = énergie cinétique maximale de l'électron + énergie du photon gamma énergie cinétique maximale de l'électron = 329,7-103 =226,7 keV. bêta - : les électrons parcourent dans la matière une plus grande distance que les rayons alpha. Ces rayons interagissent avec la matière en provoquant des excitations et des ionisations par diffusion, moindre qu'avec les rayons alpha.
- le TEL moyen maximal des particules béta -. Le transfert linéique d'énergie mesure l'énergie transféré localement au milieu cible, conséquence de la perte d'énergie de la particule chargée ; il est bien souvent égal au pouvoir d'arrêt linéique. 200 / 5,0 = 40 keV mm-1 ou 4,0 10-2 keV / micromètre = 40 eV / micromètre - l'ionisation totale IC provoquée par les particules béta -. 200 000 / 33 =6,0 103 paires d'ions. - l'ionisation spécifique ( ou densité ionique linéique) IS. Nombre de paires électron / ion crées par la particule incidente, par unité de longueur. TEL = IS w ; IS = TEL / w = 40/33 = 1,2 paire d'ion /micromètre. Energie nécessaire pour former une paire d'ions dans l'eau : w=33 eV.
Scintigraphie osseuse. Outre le technécium 99, le samarium 153 permet aussi de réaliser une scintigraphie osseuse. Le Sm 153 se trouve en unidoses de 15 mL livrées avec une activité initiale A0 = 20 GBq. La scintigraphie nécessite une dose de 370 MBq pour 10 kg de masse corporelle. En supposant que le flacon de solution contenant le samarium 153 soit en plomb, calculer l'épaiseur minimale du flacon pour arrêter 99 % des photons gamma d'énergie 103 keV. Coefficient d'atténuation m de photons d'énergie 103 keV dans le plomb m = 6,93 103 m-1. Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme : I = I0 exp (-µL) I = 0,01 I0 ; 0,01 =I0 exp (-6,93 103 L) ; ln 0,01 = -6,93 103 L ; L = ln 100 / 6,93 103 =6,6 10-4 m = 0,66 mm. Calculer le temps au bout duquel le flacon ne présente plus qu'une activité de 3 GBq. Loi de decroissance radioactive : A = A0 exp(-lt) avec l t½ = ln2 et t½ = 46 h. l = ln2/46 =1,51 10-2 h-1 ; 3 = 20 exp(-1,51 10-2t) ; ln(3/20) = -1,51 10-2t 1,897 = 1,51 10-2t ; t = 1,897 / 1,51 10-2 =125,6 heures. Calculer le volume de solution nécessaire pour effectuer cette scintigraphie sur un patient de 70 kg. ( prendre une unidose d'activité 20 GBq) La scintigraphie nécessite une dose de 370 MBq pour 10 kg de masse corporelle. 370*7 =2590 MBq = 2,59 GBq. 2,59*15 /20 =1,9 mL.
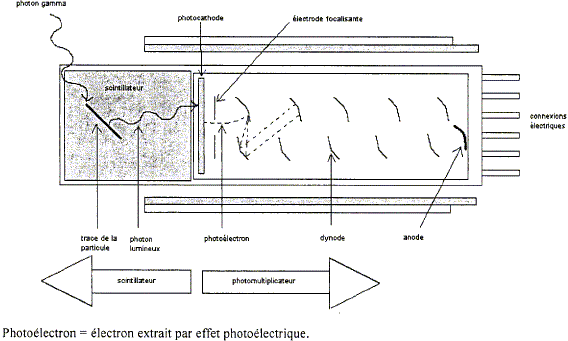
Le photomultiplieur transforme les photons issus du scintillateur en signaux électriques. Ces photons, de longueur d'onde 414 nm, arrachent à la photocathode des "photoélectrons" qui sont ensuite focalisés sur la première dynode. Le rendement quantique ( rapport du nombre de photons émis au nombre de photons reçus ) de cette photocathode est 20 %. Chaque électron frappant une dynode provoque l'émission de plusieurs électrons dits électrons secondaires. Chaque dynode multiplie par K=5 le nombre d'électrons reçus. Le photomultiplieur comporte 10 dynodes. Les électrons émis par cette dixième dynode arrive sur l'anode et génère le courant anodique dont l'intensité est de 24,0 mA. Calculer le nombre d'électrons NeA collectés par l'anode par seconde. I=24,0 mA = 2,40 10-2 A ; t = 1 s ; quantité d'électricité Q = It =2,40 10-2 C Nombre d'électrons : 2,40 10-2 /1,6 10-19 =1,50 1017. Calculer le nombre d'électrons NeP émis par la photocathode par seconde. Les 10 photodynodes effectuent une multiplication par : 510 = 9,76 106. 1,50 1017 / 9,76 106 =1,536 1010 ~1,54 1010. Calculer le nombre de photons NpP reçus par la photocathode par seconde. Le rendement est de 0,2 d'où : 1,536 1010/0,2 = 7,68 1010. En déduire la puissance du rayonnement reçu par la photocathode. Energie d'un photon : 4,8 10-19 J ; nombre de photons reçus par seconde : 7,68 1010. Puissance : 4,8 10-19 *7,68 1010 = 3,7 10-8 W.
|
|||||||||||||||||||||||||||||||||||||||||
|
|