Examen radiologique et examen échographique d'après DTS IMRT 07

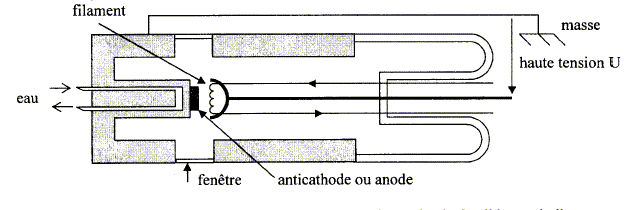
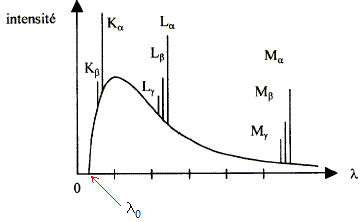
Examen radiologique :  Un tube de Coolidge, dont le schéma est proposé ci-dessus, est alimenté par une tension U = 75 kV. On donne un exemple de spectre des rayons X produits. On donne : milieu muscles os cofficient linéique d'atténuation des rayons X utilisés m (cm-1) mm =0,233 mos =0,527 Expliquer le phénomène à l'origine du fond continu du spectre d'émission des rayons X. Expliquer le phénomène à l'origine de la production de photons d'énergie donne qui forme les raies La, Lb, Ka, Kb. Les électrons freinés par les atomes de la cible conduisent à un rayonnement continu de freinage ( une partie du spectre de ce rayonnement est dans le domaine des rayons X). Ces photons X excitent les atomes de la cible : ces derniers réémettent un rayonnement X caractéristique ( spectre de raies). Que signifie les notations La, Lb, Ka, Kb ? compléter. Donner sans démonstration la relation entre la tension U d'alimentation du tube et l'énergie maximale Emax des rayons X produits. Emax = eU = 75 keV = 75 000*1,6 10-19 J = 1,2 10-14 J. En déduire la longueur d'onde minimale lmini des photons X produits. Emax = hc/ lmini ; lmini= hc/Emax lmini=6,63 10-34*3 108 / 1,2 10-14 = 1,66 10-11 m. Sachant que les photons les plus nombreux ont une longueur d'onde l=1,5 lmini , calculer l'énergie de ces photons en keV. E = hc/ (1,5lmini ) = Emax /1,5 = 75/1,5 =50 keV. Calculer le pourcentage de rayons X qui traverse 2 cm de muscle. Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme : I = I0 exp (-µL) I0 : flux de rayons X incident ; I : flux de rayons X sortant ; µ : coefficient d'atténuation linéique du milieu ; L : épaisseur du milieu traversé. exp (-mmL) = exp (-0,233*2) =0,627 ; I = 0,627 I0 ; 62,7 %. Calculer le pourcentage de rayons X qui traverse 3 cm d'os. exp (-mosL) = exp (-0,527*3) =0,206 ; I = 0,206 I0 ; 20,6 %. Calculer le contrastre radiologique C entre les milieux muscles-os si les rayons X traversent 2 cm de muscles ou 3 cm d'os. exp (-mmL) -exp (-mosL) = 0,627-0,206 =0,421 exp (-mmL)+exp (-mosL) = 0,627+0,206 =0,833 C = [exp (-mmL) -exp (-mosL) ] / [exp (-mmL)+exp (-mosL)] =0,421/ 0,833 =0,50. Le contraste radiologique est suffisant. Examen échographique. On utilise des ultrasons de fréquence 1 MHz à la même interface muscle-os ( on négligera l'épaisseur de la graisse et de la peau). On donne : milieu coefficient d'atténuation des ultrasons de fréquence 1 MHz (m-1) masse volumique kg m-3 célérité des ultrasons m s-1 muscle 26,2 1,04 103 1580 os 263 1,65 103 4000 Rappeler l'expression de l'impédance acoustique Z d'un milieu en fonction de la masse volumique du milieu et de la célérité de l'onde acoustique dans ce milieu. Z = r v. r : masse volumique kg m-3 ; v : célérité m s-1 ; Z : impédance acoustique kg m-2 s-1 ou Pa s m-1. Calculer les impédances acoustiques Zm du muscle et Zos de l'os. Zm = Z1 =rm cm =1,04 103 *1,58 103 = 1,643 106 kg m-2 s-1~ 1,6 106 kg m-2 s-1 Zos = Z2 =ros cos = 1,65 103 *4,00 103 = 6,60 106 kg m-2 s-1 Lorsqu'une onde ultrasonore arrive perpendiculairement à la surface de séparation de deux milieux d'impédance acoustique respective Z1 et Z2, on rappelle que les coefficients de réflexion et de transmission sont donnés par : aR = (Z2-Z1)2 /(Z2+Z1)2 ; aT = 4Z2Z1 /(Z2+Z1)2 . Calculer les coefficients de réflexion et de transmision à une interface muscle-os. (Z2+Z1)2 = (1,643+6,60)2 1012 =67,95 1012 . (Z1-Z2)2 = (1,643-6,60)2 1012 =24,57 1012 . aR =24,57 /67,95 =0,362. 4Z2Z1 = 4*1,643*6,60 1012 =43,37 1012. aT =43,37 /67,95 =0,638. La sonde envoie une salve d'ultrasons d'intensité acoustique I0 dans le milieu constitué de 2 cm de muscle puis 3 cm d'os. Calculer la durée qui sépare l'émission de la salve de la réception de l'écho dû à l'interface muscle-os. Les ultrasons parcourent 4 cm = 0,04 m dans le muscle à la célérité v = 1580 m/s. durée = 0,04 / 1580 = 2,53 10-5 s. Calculer l'intensité acoustique de l'écho reçu par la sonde exprimée en pourcentage de I0.  Multiplier le coefficient d'atténuation dans le muscle par l'épaisseur du muscle 2*2 =4 cm = 0,04 m 26,2*0,04 =1,048. Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme : I = I0 exp (-µL) I = I0 exp (-1,048) = 0,35 I0 Multiplier par le coefficient de réflexion : aR =0,362 I = 0,362*0,35 I0 =0,127 I0 ( ~ 13 %)

retour -menu