Energie d'une réaction nucléaire, rayons X DTS IMRT 03

Un noyau AZX émet un positon d'énergie maximum Emax = 2,5 MeV. Le noyau fils 7232Ge émet un photon gamma d'énergie 0,85 MeV. AZX ---> 7232Ge* + 01e + neutrino Conservation de la charge : Z = 32+1 = 33 ( on identifie l'élément As, arsenic) Ecrire l'équation de désintégration de l'iode 131. Conservation du nombre de nucléons : A= 72. 7233As ---> 7232Ge* + 01e + neutrino. suivie de la désexcitation du noyau fils : 7232Ge* ---> 7232Ge + photon gamma. Calculer l'énergie libérée par la transformation. énergie du photon gamma + énergie maximale du positon ( l'énergie du neutrino est alors nulle) E = 2,5 + 0,85 =3,35 MeV = 3,35 106 eV 3,35 106*1,6 10-19 = 5,36 10-13 J. Calculer la masse du noyau père. Données : masse de l'électron me = 0,000555 u = 9,11 10-31 kg ; masse du noyau 7232Ge : m(7232Ge) = 71,922080 u ; 1 u = 931,5 MeV c-2. Variation de masse Dm = m(7232Ge) + me - m(7233As) Dm = 3,35 / 931,5 = 3,596 35 10-3 u m(7233As) = m(7232Ge) + me +Dm = 71,922080 + 0,000555 + 3,596 35 10-3 =71,926231 u. Rayons X. 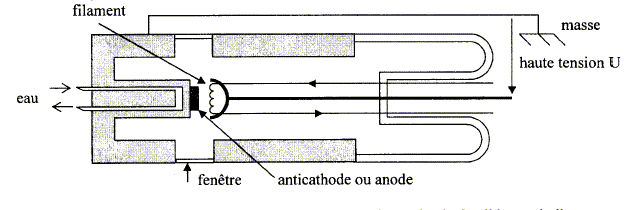Faire le schéma annoté d'un tube de Coolidge. Tube de Coolidge : tube dans lequel règne un vide poussé (environ 10-4 Pa). Les électrons sont émis par un filament de tungstène chauffé par un courant électrique (effet Joule). Le filament joue le rôle de cathode. On établit entre la cathode et l'anode une tension élevée ; celle-ci accélère les électrons émis par le filament. Les électrons accélérés frappent l'anode. La plus grande partie de la puissance électrique (99 %) est dissipée sous forme de chaleur dans l'anode. Les tubes sont refroidits par une circulation d'eau. Pourquoi l'anode est-elle généralement réalisée en tungstène ? Ce métal supporte d'assez haute température : son point de fusion est voisin de 3422 °C Un tube de rayons X fonctionne sous une tension de 250 kV. Calculer la vitesse des électrons atteignant la cible. ( On admet que les électrons ne sont pas relativistes) Energie cinétique finale des électrons : ½mev2 = eU = 1,6 10-19 *250 000 =4,0 10-14 J. v = [2eU/me]½ =[2*1,6 10-19 * 250 103 / 9,11 10-31]½ =2,96 108 m/s. Cette valeur est proche de c= 3 108 m/s ; ces électrons sont donc relativistes. En réalité ces protons sont relativistes. Dans ce cas Ec = (g-1) mc2. On donne g = (1-b2)-½ avec b = v/c. Calculer g, b puis la vitesse réelle v des électrons. g-1 = Ec /(mc2) = 4,0 10-14 /(9,11 10-31 *9 1016) = 0,488 ; g = 1,488. g = (1-b2)-½ ; (1-b2)½ = 1 / 1,488 = 0,6721 ; 1-b2 = 0,4517 ; b2 =1-0,4517= 0,5483 ; b = 0,74 ; v = 0,74 c = 0,74*3 108 = ~ 2,2 108 m/s.   Calculer la longueur d'onde minimale des rayons X émis. l mini = hc/E = 6,62 10-34*3 108 / 4 10-14 = 4,96 10-12 ~ 5,0 10-12 m. Le rendement du tube est 2%. Définir le rendement h. Puissance rayonnée par les rayons X / puissance électrique consommée * 100. Le rendement est donné par l'expression h = k Z U. Que représente k, Z et U ? Calculer k. Z : numéro atomique du tungstène Z =74 ; U haute tension appliquée entre anode et cathode. k : constante de proportionnalité. k = 0,02 / (74*250 000) = 1,1 10-9. Lors d'une radiographie, l'intensité du courant qui traverse le tube est 80 mA pour un temps de pose de 0,6 s. Déterminer la puissance du tube. P = Ui = 250 000*0,080 = 2 104 W = 20 kW. Déterminer la puissance rayonnée. 2,0 104 *0,02 = 400 W. Déterminer le nombre d'électrons ayant frappés l'anode. Quantité d'électricité Q = It = 0,08*0,6 = 4,8 10-2 C. 4,8 10-2 / 1,6 10-19 =3,0 1017 électrons.

retour -menu