Activité d'une source radioactive, l'iode 131 DTS IMRT 03

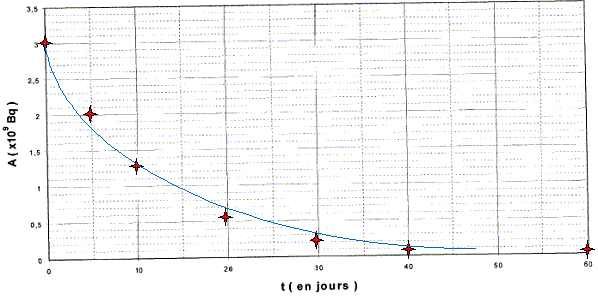
L'iode 13153I se désintègre en xénon Xe ( Z= 54) 13154Xe ; il est utilisé comme traceur gamma dans le corps humain. Sa période radioactive est de 8,1 jours. Le 1er mars 2002 à 12 h ( t=0), un établissement reçoit un échantillon d'iode 131 d'activité 3,0 109 Bq. Ecrire l'équation de désintégration de l'iode 131.  13153I --> AZX + 13154Xe. conservation de la charge : 53 =54 +Z d'où Z = -1 conservation du nombre de nucléons : 131 =A+131 ; A=0 13153I --> 0-1e + 13154Xe. Préciser l'origine du rayonnement gamma. Le noyau fils 13154Xe est souvent obtenu dans un état excité (niveau d'énergie élevé). Ce noyau dans cet état excité est en général noté Y*. Le noyau fils ne reste pas dans cet état instable. Il libère cette énergie excédentaire en émettant un rayonnement électromagnétique g. Ecrire la formule donnant l'activité A(t) d'un échantillon. Soit un échantillon dont l'activité est A0 à la date t0 =0 choisie comme date initiale. Soit A(t) l'activité à la date t et l la constante radioactive. A(t) = A0 exp(-lt). A0 : activité initiale ; l : constante radioactive ( jour-1) ; t : temps en jour. Compléter le tableau suivant et tracer A(t) pour 0< t <= 60 jours. t(j) 0 5 10 20 30 40 60 A*109 Bq 3,0 2,0 1,3 0,54 0,23 0,10 0,018 Il faut calculer l en jour-1 : l t½ = ln2 ; l = ln2 / 8,1 =8,557 10-2 j-1. A(5) = 3,0 109 exp(-8,557 10-2*5) =1,96 109 Bq ; A(10) = 3,0 109 exp(-8,557 10-2*10) =1,27 109 Bq A(20) = 3,0 109 exp(-8,557 10-2*20) =0,54 109 Bq ; A(30) = 3,0 109 exp(-8,557 10-2*30) =0,23 109 Bq A(40) = 3,0 109 exp(-8,557 10-2*40) =0,10 109 Bq ; A(60) = 3,0 109 exp(-8,557 10-2*60) =0,018 109 Bq En utilisant la courbe, déterminer la date à laquelle on observe une activité de 1,0 109 Bq. Retrouver ce résultat par le calcul.  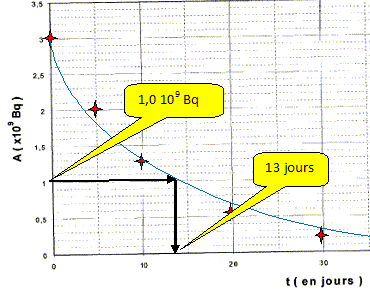1,0 109 = 3,0 109 exp(-8,56 10-2 t) ln 1/3 = -8,56 10-2 t ; t =12,8 ~ 13 jours.   Calculer la masse d'iode présent dans l'échantillon le 31 mars à 12 h. La différence des dates donne t = 30 jours. Activité à la date t = 30 jours : A(30) = A0 exp(-8,56 10-2*30) = 7,67 10-2 A0. L'activité et la masse sont proportionnelles ; il reste le 31 mars 7,67 % de la masse diode 131 initiale. Calcul de la masse initiale m0 : Exprimer la constante radioactive en s-1 : 8,1 j = 8,1*24*3600 = 7,0 105 s. l = ln2 / 7,0 105 = 9,9 10-7 s-1; Nombre initiaux de noyaux : N0 = A0/l =3,0 109 / 9,9 10-7 = 3,0 1015 noyaux Quantité de matière (mol) : n = N0 /NA =3,0 1015 / 6,02 1023 =5,0 10-9 mol Masse molaire de l'iode 131 : M= 131 g/mol m0 =n M= 5,0 10-9 *131 =6,6 10-7 g. masse restante le 31 mars à 12 h : =6,6 10-7 * 0,0767 =5,1 10-8 g.

retour -menu