Le cyclotron d'après DTS IMRT 00

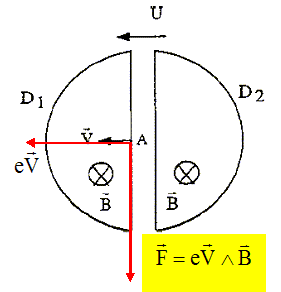
Les accélérateurs de type cyclotron permettent d'obtenir des particules chargées lourdes (protons, deutons...) de haute énergie susceptibles de provoquer des réactions nucléaires. Un cyclotron comporte deux demi cylindres creux Dl et D2 appelés les "dees". A l'intérieur des dees, règne un champ magnétique B uniforme et constant tel que B = 1,8 T. Entre les dees, il existe un champ électrique E produit par la différence de potentiel électrique U. Des deutons 21H sont injectés dans Dl en A avec une vitesse V perpendiculaire à B. Représenter la force magnétique qui s'exerce sur un deuton en A. Les deutons ont une charge positive gale à la charge élémentaire. 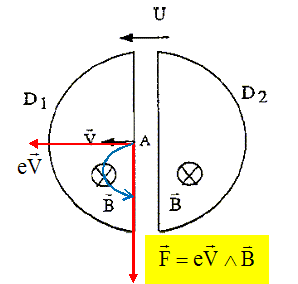De quel type est le mouvement des deutons dans Dl ? Représenter la trajectoire correspondante en indiquant le sens du mouvement. Mouvement circulaire uniforme. Exprimer littéralement la durée du mouvement d'un deuton dans D1. Cette durée dépend-elle de la vitesse en A ? Effectuer l'application numérique. 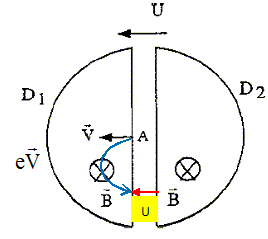On donne : masse d'un deuton : m=2,014 u ; 1 u =1,67 10-27 kg ; e = 1,6 10-19 C. Les protons parcourent une demi circonférence de rayon r à la vitesse v de valeur constante : p r = V t½ avec r = mV/(eB) soit t½= p r / V = m/(eB), indépendant de la vitesse en A. t½ =2,104*1,67 10-27 / (1,6 10-19 *1,8) =1,22 10-8 s. Quel doit être le sens du champ électrique entre les dees pour que les deutons soient accélérés à leur sortie de D1 ? Le représenter.  Le travail de la force électrique doit être moteur : W = eUD1D2 avec UD1D2 >0. Quel est alors le signe de la tension U entre les dees ? La tension VD1-VD2 est positive. Les deutons pénètrent dans D2 en un point C. Décrire leur mouvement. Quel est le temps de parcours dans D2 ? Les deutons ne sont soumis qu'à la force magnétique : ils sont animés d'un mouvement circulaire uniforme à une vitesse V1. La durée du parcours de la demi-circonférence est indépendant de la vitesse et vaut donc 1,22 10-8 s. Ils sortent de D2 en C'. Quels doivent être le sens du champ électrique et le signe de la tension U entre les dees pour qu'ils soient à nouveau accélérés ? 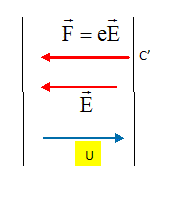La tension accélératrice doit avoir changé de sens en C'. Calculer la fréquence de la tension alternative qu'il faut appliquer entre les dees. La durée de passage entre les dees est négligeable devant la durée du trajet dans chaque dee. Pour une accélération maximale, à chaque demi tour, la tension alternative doit changer de signe et prendre sa valeur maximale. La demi période de la tension alternative est égale à la durée d'un demi tour. T = 2t½ = 2p m / (eB). f = 1/T = eB /(2p m). f = 1/(2*1,22 10-8 ) =4,1 107 Hz. Les deutons, supposés non relativistes, continuent ainsi leur mouvement de plus en plus rapidement ; ils sont extraits du cyclotron lorsque le rayon de la trajectoire dans les dees atteint la valeur Rm = 0,40 m Calculer leur énergie cinétique en joule, puis en MeV. r = mV/(eB) ; V = eB r / m = 1,6 10-19*1,8*0,4 / (2,104*1,67 10-27)=3,3 107 m/s. Energie cinétique : ½mV2 =0,5*2,104*1,67 10-27 *(3,3 107)2 =1,9 10-12 J. 1,9 10-12 /1,6 10-19 =1,18 107 eV ~ 12 MeV.

retour -menu