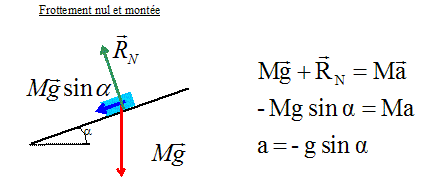|
A un instant pris comme origine des dates, un solide
de masse m=200g passe à l'extrémité A
d'un plan incliné d'un angle de 25° par rapport
à l'horizontale, avec une vitesse V0=3,6
m/s et s'élève le long de ce plan
incliné.
Dans un premier temps, on considère les
frottements comme négligeables.
Déterminer les
caractéristiques du vecteur
accélération, en dédire la nature du
mouvement.
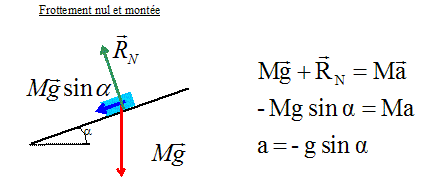
L'accélération est parallèle au
plan, dirigée vers le bas.
a = -9,8 sin 25 = -4,1 m s-2.
Le mouvement est rectiligne uniformément
décéléré.
|
|
A quelle date, le
mobile aura-t-il une vitesse de 2m/s ?
La vitesse est une primitive de
l'accélération :
v(t) = -at + vitesse initiale
v(t) = -4,14 t + 3,6.
t = (3,6-2) / 4,14 =
0,39 s.
|
Quelle distance parcourt-il
en 0,8 s ?
La position est une primitive de la vitesse : x(t) =
-½at2 + 3,6 t + position initiale.
x(t) = -2,07 t2 + 3,6 t.
x(0,8) = -2,07 *0,82 + 3,6 *0,8 =
1,55 m.
|
|
En réalité une force de
frottement f opposée au déplacement
et de valeur 0,045 N s'exerce sur le solide pendant
la montée.
En utilisant le
théorèmede l'énergie
cinétique, déterminer la distance AC
parcourue par le mobile jusqu'à ce qu'il
rebrousse chemin.
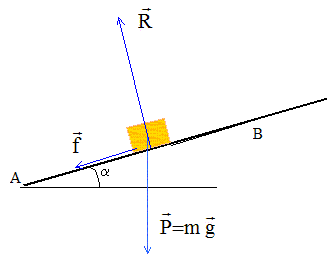
Travail résistant du poids en
montée :
-mg AC sin 25 = 0,2*9,8*AC * sin 25 = -0,828 AC
joules.
Travail résistant de la force de
frottement :
-f AC = -0,045 AC joules
L'action du plan R, perpendiculaire à la
vitesse, ne travaille aps.
Total des travaux : -0,873 AC joules.
Variation de l'énergie cinétique
entre le bas du plan et l'arrêt ( avanr
desente).
0 - ½mv02 =
-0,5*0,2*3,62 = -1,296 J
La variation de l'énergie
cinétique est égale à la somme
des travaux des forces :
-1,296 =-0,873 AC ; AC = 1,296/0,873
~1,5 m.
|
|