|
conductivité dans un métal et dans un semi-conducteur : concours général 2008 |
|||||||
|
|||||||
|
Les vecteurs sont écrits en gras et en rouge.
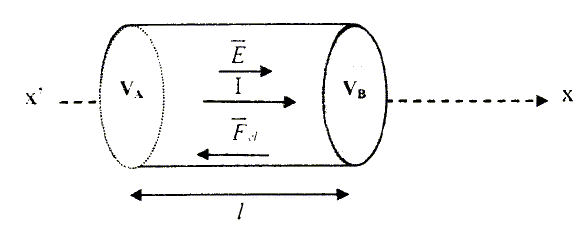
On établit à l'instant t=0, une différence de potentiel constante VA-VB >0 entre les deux extrémités d'un barreau cylindrique en cuivre de longueur L, de section S et d'axe x'x. Le barreau est le siège d'un courant d'intensité I qui résulte du déplacement des électrons libres présents dans le métal. Ces électrons sont mis en mouvement sous l'effet d'une force électrique Fel, dirigée en sens contraire du courant I et qui s'écrit Fel = -eE. ( E champ électrique permanent et uniforme qui règne à l'intérieur du barreau). La norme du champ électrique vaut E = (VA-VB ) / L. Ces électrons libres évoluent dans un réseau de charges quasiment immobiles et ne sont donc pas complètement libres. Pour rendre compte du rôle essentiel du milieu, Drude a proposé d'introduire une force de frottement visqueux, opposée à la vitesse de l'électron v, de la forme F = -kv avec k une constante positive caractéristique du milieu. En appliquant la seconde loi de Newton à l'électron, déterminer l'équation différentielle vérifiée par chacune des coordonnées de la vitesse d'un électron. Fel + F = m dv /dt ; sur l'axe x'x : -eE-k v = mdv/dt. dvx/dt + k/m vx = -e/m E. solution générale de l'équation sans second membre : vx = B exp(-k/m t) solution particulière ( régime permanent ) : vx =-e/k E solution générale de l'équation avec second membre : vx = B exp(-k/m t)-e/k E. à t=0, la vitesse est nulle : 0 = B-e/k E. vx = -e/k E [ 1-exp(-k/m t)]. vy =Cste exp(-k/m t). dvz/dt + k/m
vz =0 vz =Cste exp(-k/m t). En déduire que
la vitesse d'un électron libre peut
s'écrire
v
= -
µ
E
après un certain temps
caractéristique que l'on exprimera en
fonction de
m
et
k. En régime permanent , les deux forces se
compensent et la valeur de la vitesse est
constante. Fel
+ F
=0 ;
-eE - k
v
=0 ;
vx =
-e/kE ;
vy
=0 ;
vz
=0. La mobilité caractéristique de
l'électron A vaut :
µ
= e/k. Le vecteur densité de courant j est défini par j = rm v avec rm la densité volumique de charges mobiles et v la vitesse de l'électron libre. La densité volumique de charges mobiles peut s'écrire rm = - n e où n représente le nombre d'électrons libres par unité de volume. Exprimer la conductivité g du métal définie par la loi d'Ohm locale j = gE en fonction de n, e et de la mobilité µ. On note j la norme du vecteur densité de courant. d'une part : j = rm v = -n e v ; d'autre part v = - µ E ; par suite j = n e µ E ; On identifie g = n e µ . L'intensité I du courant représente la quantité d'électricité qui traverse la section S par unité de temps. Elle s'exprime de façon simple dans notre cas particulier par la relation I = j S où S désigne la section du barreau. En déduire la résistance RAB du barreau du cuivre en fonction de g, S et L ? d'une part j = g E ; d'autre part E = (VA-VB)/L et enfin I = j S : I = g (VA-VB) S/L ; RAB =(VA-VB)/ I = L/ (gS). Quelle est l'unité de g ? g = L/(RAB S) ; [g] =m /( W m2) = W-1 m-1. Remarque : la résistivité r est l'inverse de la conductivité g.
Dans un semi-conducteur d'arséniure de gallium dopé N, le phénomène de conduction est dû à la présence de n=ND =1,5 1021 électrons par m3 apportés par les atomes de silicium. Ces électrons possèdent une mobilité µ- =9200 cm2V-1 s-1. Calculer numériquement la conductivité g du semi-conducteur d'arséniure de gallium dopé N. µ- =9200 cm2V-1 s-1 = 9200 10-4 m2V-1 s-1 =0,92 m2V-1 s-1. g = n e µ =1,5 1021 *1,6 10-19 *0,92 =221 W-1 m-1. Pour réaliser de l'arséniure de gallium dopé P, on a incorporé à de l'arséniure de gallium pur, du zinc à raison de NA =3 1023 atomes de zinc par m3 d'arséniure de gallium.
|
|||||||
|
|