diode électroluminescente : dopage, diffusion loi de Fick : concours général 2008

Pour réaliser de l'arséniure de gallium AsAG dopé N, on a incorporé à de l'arséniure de gallium pur, du silicium, à raison de ND =1,5 1021 atomes de silicium par m3 d'arséniure de gallium. On suppose que les atomes de silicium sont régulièrement répartis dans le cristal d'arséniure de gallium. Calculer le nombre de moles d'arséniure de gallium par m3. On donne la masse volumique de l'arséniure de gallium : rGa = 5318 kg m-3 ; Ga : 69,7 ; As : 75 g/mol. Masse molaire AsGa : M = 75+69,7 = 144,7 g/mol. masse de 1 m3 : m = 5,318 106 g. Quantité de matière n = m/M = 5,318 106 /144,7 = 3,68 104 moles dans 1 m3. Pour un volume donné d'arséniure de gallium de type N, calculer le rapport du nombre de moles d'arséniure de gallium au nombres de moles d'atomes de silicium. Quantité de matière de silicium dans 1 m3 : ND / NA =1,5 1021 /6,02 1023 =2,49 10-3 mole dans 1 m3. 3,68 104 /2,49 10-3 =1,48 10-7. Evaluer numériquement la masse de silicium à incorporer à 1 kg d'arséniure de gallium pour obtenir la concentration ND indiquée. M(Si ) =28 g/mol. Quantité de matière n(AsGa) = m/M = 1 103 /144,7 = 6,91 moles Quantité de matière n(Si) =n(AsGa)/1,48 107 =6,91 /1,48 107 =4,68 10-7 mol masse m = n(Si) *M(Si) = 4,68 10-7 *28 =1,31 10-5 g. Le dopage : Une technique de dopage des semi-conducteurs est la diffusion moléculaire d'impuretés à l'état gazeux au sein du réseau cristallin du semi-conducteur d'arséniure de gallium. On va étudier une situation simple à une dimension et on va supposer le régime permanent ( c'est à dire indépendant du temps). On impose à l'extrémité x=0 d'un cylindre d'arséniure de gallium de section S un nombre n1 d'atomes de silicium par m3 et à l'autre extrémité x=L un nombre n2 d'atomes de silicium par m3 (n2 <n1). La distribution des atomes de ilicium n'étant pas homogène, les atomes diffusent à l'intérieur du cylindre dans le sens des x croissant. La densité de courant de diffusion jn est égale au nombre d'atomes traversant par unité de temps une unité de surface perpendiculaire à l'axe Ox. Quelle est l'unité de jn ? surface en m2 et temps en seconde ( m-2 s-1) Soit n(x) le nomre d'atomes de Si par unité de volume à l'abscisse x. L'expérience montre que l'on peut utiliser avec une excellente approximation la loi de Fick : jn = -D dn(x) / dx où D est une constante. Expliquer pourquoi D est une constante positive. Quelle est l'unité de D ? n2 <n1 : dn est donc négatif ; de plus jn est positif donc D est positive. [jn ] =m-2 s-1 ; [dx] = m ; [dn(x)] = m-3 ; [D]=[-jndx/dn(x)]= m-2 s-1 m m3 = m2 s-1. Considérons un cylindre élémentaire de section S compris entre les plans d'abscisses x et x+dx : Exprimer le nombre d'atomes de silicium dN(x) entrant de la face d'abscisse x pendant le temps dt en fonction de S, dt et jn(x). nombre d'atomes traversant par unité de temps une unité de surface perpendiculaire à l'axe Ox : jn(x). nombre d'atomes traversant pendant la durée dt une surface S perpendiculaire à l'axe Ox : dN(x)= jn (x)S dt. Exprimer le nombre d'atomes de silicium dN(x+dx) sortant de la face d'abscisse x+dx pendant le temps dt en fonction de S, dt et jn(x+dx). nombre d'atomes traversant par unité de temps une unité de surface perpendiculaire à l'axe Ox : jn (x+dx). nombre d'atomes traversant pendant la durée dt une surface S perpendiculaire à l'axe Ox : dN(x+dx)= jn(x+dx) S dt. Ecrire une relation traduisant la conservation de la quantité de matière pour le cylindre élémentaire en régime permanent. Le régime permanent est indépendant du temps : le nombre d'atomes de silicium entrant dans le cylindre élémentaire est égal au nombre d'atomes de silicium sortant : dN(x)= dN(x) ; jn (x) = jn(x+dx) = constante. Donner la loi simple vérifiée par n(x) en fonction de n1, n2, L et x. dn(x) = -jn / Ddx , intégrer entre x=0 et x : n(x) -n(0) =n(x) -n1 = -jn / D x ; de plus n(L) - n(0) = n2-n1 = -jn L / D ; jn / D = (n1-n2)/L d'où : n(x) -n1 =-(n1-n2) x /L ; n(x)= n1-(n1-n2) x /L. Considérons à présents la situation expérimentale dans laquelle les atomes de silicium sont à la date t=0, introduits brusquement en x=0 dans le semi-conducteur d'arséniure de gallium. Soit N0 le nombre d'atomes de silicium ainsi introduits par unité de surface à t=0. 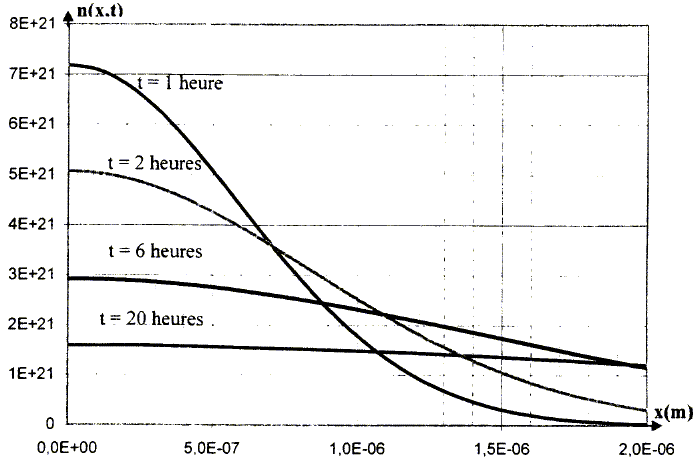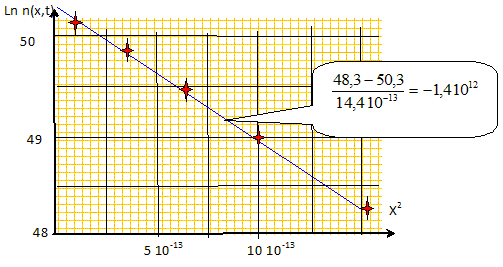On peut montrer que le nombre d'atomes de silicium n(x,t) par unité de volume à l'ascisse x à l'instant t est de la forme : Le régime n'est plus permanent. En utilisant une analyse dimensionnelle, donner la dépendance du temps caractéristique t de difusion jusqu'à l'abscisse x, en fonction de x et du coefficient de diffusion D. x2/(4D t ) est sans dimension ; t a la dimension d'un temps ; donc x2/(4D) a la dimension d'un temps. t =x2/(4D). On donne quelques courbes représentant en fonction de x, la distribution n(x,t) du nombre d'atomes de silicium par m3 à différents instants t : En explicitant la méthode utilisée, en déduire le ceficient de diffusion D du silicium dans l'arséniure de gallium. A partir de la courbe correspondant à t= 1 heure, représenter ln( n(x,t)) en fonction de x2. ln(n(x,t)) = ln(N0/(4pDt)½) -x2/(4Dt), droite de pente -1/(4Dt) x 0 2 10-7 4 10-7 6 10-7 8 10-7 10 10-7 12 10-7 x2 0 0,4 10-13 1,6 10-13 3,6 10-13 6,4 10-13 10 10-13 14,4 10-13 n(x,t) 7,3 1021 7,0 1021 5,9 1021 4,5 1021 3,1 1021 1,9 1021 0,93 1021 ln n(x,t) 50,34 50,30 50,13 49,86 49,49 49,0 48,28 1,4 1012 = 1/(4Dt) avec t = 3600 s ; D = 1/ (1,4 1012 *4*3600) = 5,0 10-17 m2 s-1. Quelle est la valeur du temps caractéristique t pour une longueur de 2 micromètres ? t =x2/(4D) = 4 10-12 / (4*5 10-17) = 2 104 s ~5,6 heures. Au bout de 5t ~ 28 heures, la répartition des atomes de silicium est homogène.

retour -menu