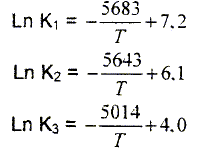L'élément tungstène de symbol W
est toujours combiné à l'élément
oxygène dans ces minerais. La dernière
étape d'élaboration du tungstène
conduit à réduire à 1173 K le trioxyde
de tungstène WO3 par le dihydrogène
selon l'équation :
WO3(s) + 3H2(g) = W(s) +
3H2O(g).
(a) constante
d'équilibre Ka = 1,9.
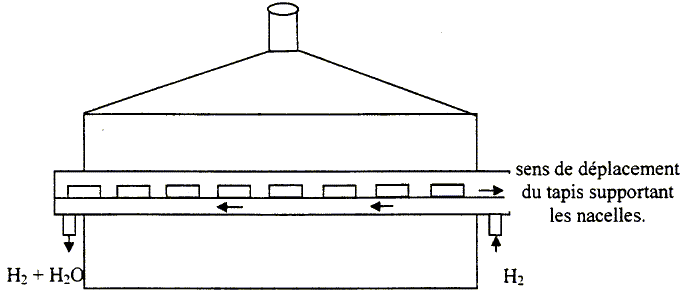
la réduction se fait dans un four
électrique dans lequel on observe un double mouvement
: le dihydrogène, pur et sec à l'entrée
en excès, passe en contre courant sur le trioxyde de
tungstène disposé dans des nacelles qui
circulent en sens inverse.
Donner une condition sur les
quantités de matière de dihydrogène et
d'eau pour que la réaction se produise dans le sens
direct.
|
Q r i < K ; Q r i
< 1,9 ;
|
n3(H2O)éq
n3(H2)éq
|
< 1,9 ;
|
n(H2O)éq
n(H2)éq
|
< 1,24
|
Le dihydrogène doit être en excès ; le
dihydrogène en excès est séché (
élimination de l'eau par condensation) ,
réchauffé puis à nouveau injecté
dans le four.
La technique du contre courant permet d'éliminer
l'eau et de travailler en continu.
En réalité, la réduction se fait
selon les trois équations suivantes :
|
|
4 WO3(s) + H2(g) =
W4O11 (s) + H2O(g)
(1)
W4O11 (s)
+3H2(g) = 4WO2 (s) +
3H2O(g)
(2)
WO2 (s) +2H2(g) = W(s)+
2H2O(g)
(3)
Dans le domaine de température 850 - 1300
K, les constantes d'équilibre des
réactions précédentes
dépendent de la température selon les
équations :( T en kelvin)
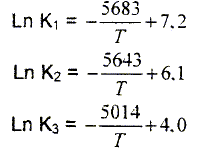
|
La relation de Van't Hoff permet de montrer que la
constante d'équilibre K d'une réaction
chimique dépend de la température selon la loi
:
ln K =
a
-E/(RT) où a
est une constante et E
l'énergie molaire de la réaction.
Calculer les énergies
molaires des 3 réactions. R = 8,31 J
K-1 mol-1.
E1 = 5683 * 8,31 = 4,72 104 J
mol-1.
E2 = 5643 * 8,31 = 4,69 104 J
mol-1.
E3 = 5014 * 8,31 = 4,17 104 J
mol-1.
Ces énergies étant positives, les
réactions sont endothermiques : elles seront
favorisées par une élévation de
température ( apport d'énergie ).
Montrer que la réaction
(a) peut se mettre sous
la forme d'une combinaison linéaire des
équations (1),
(2),
(3).
WO3(s) +0,25 H2(g) =0,25
W4O11 (s) + 0,25H2O(g)
(1)
0,25 W4O11 (s) +0,75
H2(g) = WO2 (s) + 0,75
H2O(g)
(2)
WO2 (s) +2 H2(g) = W(s)+ 2
H2O(g)
(3)
0,25 (1)
+0,25
(2) +
(3)
donnent : WO3(s) +3 H2(g) =
W(s)+ 3 H2O(g)
(a).
La température est un paramètre important
de la fabrication du tungstène comme en
témoigne l'expérience suivante :
10 g de poudre fine d'oxyde jaune de trioxyde de
tungstène WO3 sont soumis à un
courant de dihydrogène sec pendant 1 heure à
différentes températures maintenues constantes
pendant l'opération. Les résultats sont
rassemblés dans le tableau suivant :
|
température (K)
|
aspect
|
composition
|
|
900
|
brun
|
WO2
|
|
950
|
brun noir
|
WO2 + W
|
|
1000
|
gris noir
|
W
|
|
1200
|
gris métallique
|
W
|
|
1300
|
gris métallique granuleux
|
W
|
Photographies obtenues au microscope
:

|

|
|
900 K, oxyde brun WO2
diamètre des particules d = 0,5
micromètre
|
1000 K, tungstène
diamètre des particules d = 1
micromètre
|

|

|
|
1200 K, tungstène
diamètre des particules d = 3
micromètres
|
1300 K, tungstène
diamètre des particules d = 10
micromètres
|
A 900K, la réaction (3) ne se produit pas ; à
950 K la réaction (3) conduit à un
équilibre ; à une température
supérieure à 1000 K, la réaction (3)
est totale.
La température détermine également
la taille des particules.
|
|
Pour obtenir une poudre de tungstène
constituée de grains fins de l'ordre de 1
micromètre, l'industriel peut agir sur
différents paramètres.
Quelle
température faut-il choisir ?
1100 K.
Préfère
t-on :
- une faible ou une forte épaisseur de la
couche d'oxyde ?
- une faible ou une forte porosité de
cette couche d'oxyde ?
- un débit faible ou élevé
du courant d'hydrogène ?
- une faible ou une grande vitesse de passage
des nacelles contenant l'oxyde ?
Pour un meilleur contact entre les
réactifs, il faut une faible
épaisseur de la couche d'oxyde et une grande
porosité de celle-ci, un débit
important en dihydrogène. La vitesse de
passage des nacelles doit être assez faible,
afin que la réduction puisse se
réaliser de manière
homogène.
Certains auteurs ont essayé de quantifier
ces influences. Ainsi, la durée de
réduction de la couche d'oxyde en position
statique est donnée par la relation
empirique suivante :
t = 6,66 1020
r0T-5,7
(f h)1,6.
t : durée
de la réduction en seconde
r0
: masse volumique de l'oxyde g cm-3
T :
température de réduction en
kelvin
f : fraction
d'oxyde réduit
h: hauteur de la
couche d'oxyde en cm.
Commenter la
formule.
Une masse volumique faible correspond à
une poudre poreuse, réduite en un temps plus
court.
Si la température passe de 1000 à
1300 K ( 1000 -5,7 = 8 10-18
et 1300 -5,7 = 2 10-18), la
durée de la réduction est
divisée par 4.
Plus la couche est épaisse, plus
l'hydrogène met du temps pour atteindre les
couches profondes.
En passant de h = 1 cm à h = 5 cm (
11,6 = 1 ; 51,6 = 13 ) la
durée de la réduction est 13 fois
plus grande.
|