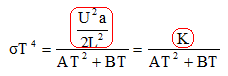La lampe à incandescence classique et la lampe halogène : concours général 2008

Ce type d'ampoule produit de la lumière en portant à l'incandescence un filament de tungstène. Ce filament, porté à haute température émet un rayonnement dont le spectre est continu, assez proche de celui du soleil. ( bon confort visuel). Tout corps porté à une température T rayonne une puissance P suivant la loi de Stefan : P = sT4 S où S représente la surface en contact avec le milieu extérieur, T sa température et s =5,67 10-8 W K-4 m-2, la constante de Stefan. Le filament est assimilé à un cylindre de longueur L= 40 cm, de raton a = 0,02 mm, de résistance R =rL/(pa2), avec r la résistivité du tungstène. L'ampoule en verre est remplie d'un gaz inerte ( argon, krypton...) afin de protéger le filament. La température de fusion du tungstène vaut Tfusion = 3683 K A 25°C, la résistivité r du tungstène vaut 7,1 10-8 W m. Pour une tension d'alimentation U= 220 V aux bornes du filament, quelle est la puissance PJ dissipée par effet Joule ? Commenter. section du filament : pa2 =3,14*(2 10-5)2 = 1,256 10-9 m2. Résistance du filament : R =rL/(pa2) = 7,1 10-8 *0,4/ 1,256 10-9 =22,6 ohms à 25°C. PJ = U2/R =2202/22,6 = 2,1 103 W, valeur élevée pour une ampoule domestique. Cette puissance dissipée par effet Joule est convertie en chaleur : la température du filament s'élève. Ce filament, porté à haute température émet un rayonnement dont le spectre est continu, assez proche de celui du soleil. Puissance Pr rayonnée par le filament en fonction de s, L, a et T. Surface latérale du filament, cylindre de rayon a et de longueur L : S = 2paL = 6,28 *2 10-5*0,4 =5,0 10-5 m2 . Loi de Stefan : P = sT4 S = sT4 2paL. Température d'équilibbre du filament : En régime permanent, la puissance Joule est égale à la puissance rayonnée : sT4 2paL = 2,1 103. 5,67 10-8 T4 * 5,0 10-5= 2,1 103. T4 = 2,37 1014 ; T = 5,2 103 K. Cette valeur est "impossible", le tungstène a fondu. En réalité la résistivité du tungstène dépend de la température suivant la loi : r = AT2 + BT avec A = 2,5 10-14 W m K-2 et B = 2,3 10-10 W m K-1. Montrer que la température d'équilibre du filament est solution d'une équation du type : où K est une constante. Calculer K, préciser son unité. 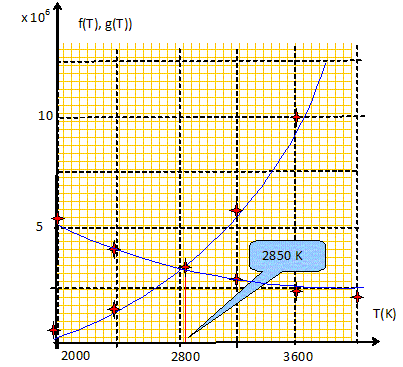Résistance du filament : R =rL/(pa2) = (AT2 + BT)L/(pa2) PJ = U2/R =U2pa2/[(AT2 + BT)L] En régime permanent, la puissance Joule est égale à la puissance rayonnée : sT4 2paL =U2pa2/[(AT2 + BT)L] ; K = U2a/ (2L2) =2202*2 10-5 / (2*0,42) = 3,0 V2 m-1. Tracer sur un même graphique les deux fonctions f(T) = sT4 et g(T) = K/(AT2 + BT) en fonction de T pour T compris entre 2000 et 4000 K. 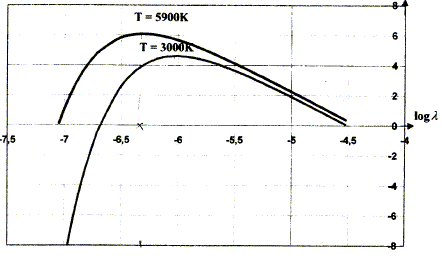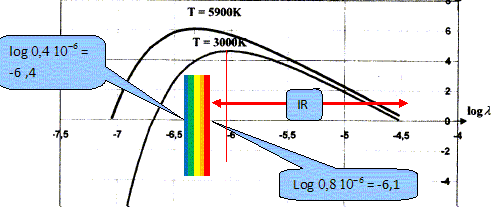T(K) 2000 2400 2800 3200 3600 4000 f(T) = 5,67 10-8 T4 9,1 105 1,9 106 3,5 106 5,9 106 9,5 106 1,5 107 g(T) = 3/(2,5 10-14T2 + 2,3 10-10 T 5,4 106 4,3 106 3,6 106 3 106 2,6 106 2,3 106 La température réelle du filament est voisine de 2850 K, inférieure à la température de fusion : le filament reste solide. Le filament est torsadé et sa longueur, proche de 40 cm, permet d'obtenir une température élevéée tout en restant inférieure à la température de fusion. Le tungstène est le seul métal à posséder une température de fusion très élevée, d'où son choix. Rendement. La température de surface du soleil est de l'ordre de 5900 K ; le soleil émet un rayonnement dont le spectre admet un maximum d'émission pour la longueur d'onde lm = 0,49 micromètre. L'énergie par unité de surface et par unité de longueur d'onde, associée au rayonnement émis, est appelée densité spectrale d'énergie volumique rayonnée. Elle est notée u et s'exprime en J m-4. On donne les courbes suivantes pour deux corps portés aux températures respectives 5900 K et 300 K. 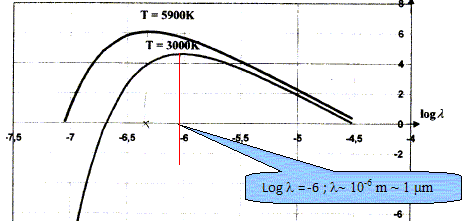Dans quel domaine spectral se situe la longueur d'onde lm ? Le domaine visible s'étend de 0,4 micromètre à 0,8 micromètre : 0,49 micromètre appartient au domaine visible. A partir du graphique, évaluer la longueur d'onde correspondant au maximum de la puissance émise par le filament. A quel domaine spectral appartient-il ? 1 micromètre appartient au domaine des infrarouges ( IR). On constate que 95 % de la puissance lumineuse émise par le filament n'est pas dans le domaine visible. Seulement 5 % de la puissance rayonnée se trouve dans le domaine visible. 95 % de la puissance est convertie en chaleur. Rendement de la lampe = puissance émise dans le visible puissance totale émise = 5%. Le rendement d'une lampe à incandescence est très faible. Les lampes halogènes sont des lampes à incandescence. Elles possèdent en plus les propriétés suivantes : - durée de fonctionnement de l'ordre de 2000 heures ( le double d'une lampe à incandescence classique) - une efficacité lumineuse bien supérieure. Le cycle halogène peut se traduire par l'équation suivante : ( W est un atome de tungstène, X un atome d'halogène, iode ou brome) W + 2X = WX2. A basse température ( vers 573 K) la réaction est totale dans le sens direct et à haute température ( vers 3000 K) la réaction peut être considérée comme totale dans le sens inverse. Dans une première étape, certains atomes de tungstène du filament se subliment. A bonne distance du filament, là où la température est plus faible ( 573 K) les atomes de tungstène se combinent aux molécules d'halogènes ( réaction dans le sens direct). Les molécules ainsi formées, se rapprochant du filament à 3000 K se décomposent ( réaction dans le sens inverse) et les atomes de tungstène peuvent se redéposer sur le filament. La température est un facteur important pour décrire le sens d'évolution d'un système chimique. En vous basant sur un exemple de votre choix, citer un autre paramètre permettant d'influer le caractère total ou limité d'une réaction chimique. La quantité de matière (mole) de l'un des réactifs ou de l'un des produits. On déplace un équilibre dans le sens direct : ( estérification par exemple) - en ajoutant un réactif en excès, - en éliminant un produit au fur et à mesure qu'il se forme. La température du filament d'une lampe halogène étant plus élevée que dans le cas d'une lampe à incandescence classique, quel éclairage va préférer l'utilisateur ? Justifier. 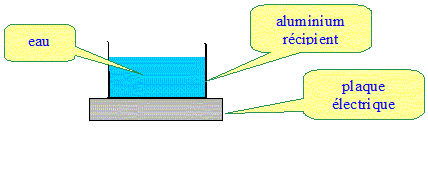Le spectre de lampe halogène se rapproche du spectre solaire : l'utilisateur préfèrera l'éclairage halogène. Un corps chauffé émet de l'énergie sous forme de rayonnement électromagnétique. Connaissez vous d'autres modes de transfert thermiques ? Le transfert thermique entre la plaque et le récipient s'effectue par conduction. Le transfert thermique entre le récipient et l'eau s'effectue par conduction. Au sein du liquide, la température n'est pas identique en tous points : en conséquence, l'eau la plus chaude ( au fond) a une masse volumique plus faible que l'eau plus froide de surface. On observe des déplacements du liquide ou courants de convexion. Quelle différence importante y a-t-il avec les précédents ? conduction : transfert d'énergie par contact entre un corps chaud et un corps froid. convexion : transfert d'énergie avec déplacement de molécules dans un fluide. Au vu de ces quelques données, il semble donc qu'un filament puisse durer indéfiniment, en réalité le tungstène a une fâcheuse tendance à se redéposer à un endroit différent de celui d'où il vient. Il apparaît donc une série de points fragiles sur le filament. Ces points sont des zones de rupture potentielles. Pourquoi les zones de faible section sont-elles plus chaudes ? La résistance R = r L/s est d'autant plus grande que la section s est plus faible : la puissance consommée par effet joule PJ = RI2 va donc augmenter et en conséquence la température sera plus élevée. Ces zones plus chaudes sont moins aptes à recevoir du tungstène et la fragilisation est ainsi encore accélérée en fin de vie du filament.

retour -menu