|
Thermomètre réparti à effet Raman : concours général 2006 |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
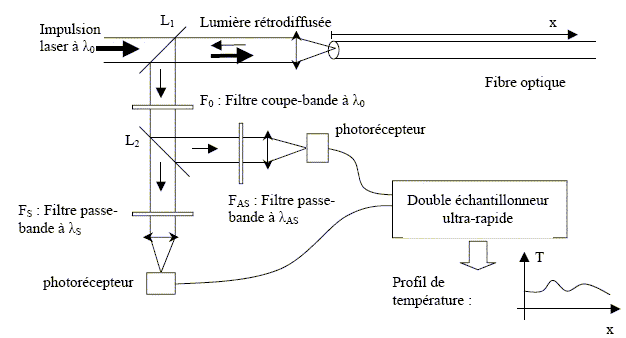
Surveillance de sites à risques : Les thermomètres répartis à effet Raman permettent la surveillance efficace de câbles électriques souterrains THT ( très haute tension), comme par exemple la ligne électrique triphasée 400 kV alimentant l'aéroport de Manchester en Angleterre. On transporte l'énergie électrique sous THT afin d'éviter les pertes par effet Joule, en ligne. (l'intensité est plus faible si la tension est élevée). Le coût d'une ligne THT souterraine est très élevé, on préfére le transport aérien ; par contre dans certains sites ( aéroport) , une ligne aérienne présente un risque d'accident trop grand, on l'enterre donc. Le tunnel du Mont Blanc (11,6 km de long) est équipé d'un tel système de surveillance. Description du thermomètre. Un laser envoie dans la fibre optique ( le long de laquelle sera mesurée la température) des impulsions lumineuses très courtes de durée t0. On suppose que cette lumière est monochromatique de fréquence n0. Lors de la propagation de cette impulsion, une partie de la lumière va être diffusée par les défauts situés à l'intérieur de la fibre. La plupart de cette lumière diffusée est envoyée hors de la fibre, mais une petite proportion est recapturée par le coeur et se trouve guidée dans le sens opposé à l'onde incidente : il s'agit de la lumière rétrodiffusée. Une lame séparatrice L1 permet de récupérer la moitié de la lumière rétrodiffusée. Le filtre coupe bande F0 bloque la raie principale correspondant à l0 et la lame séparatrice L2 permet de dédoubler le faisceau. Le filtre passe bande FS laisse passer uniquement la raie Stokes et le filtre FAS la raie anti-Stohes. Les deux photorécepteurs permettent de mesurer l'intensité de chacune des deux raies. La mesure du rapport des intensités permet d'avoir accès à la température.
Dans la fibre la vitesse de l'impulsion est v = c/n avec n : indice de réfraction du coeur de la fibre. La distance x est aprcourue en une durée t = x/v =x n / c. On observe la lumière rétrodiffusée ( à la distance x), à la date 2t = 2 x n/c. Si la durée de l'impulsion est assez grande : la lumière rétrodiffusée peut provenir d'un distance x atteinte par le début de l'impulsion ou provenir d'une distance y atteinte à la fin de l'impulsion ; il en résulte une imprécision sur la distance. La durée de l'impulsion doit être faible pour avoir une précision de l'ordre du mètre. Durée maximale de l'impulsion. 2t1 = 2xn/c ; 2t2 = 2yn/c ; 2t2-2t1 =2n/c(y-x) avec y-x ~ 1 m ; on donne n = 1,5 et c = 3 108 m/s. 2t2-2t1 = 2*1,5/3 108 = 10-8 s = 10*10-9 s = 10 nanosecondes. De plus, le système d'acquisition électronique ( c'est à dire la mesure périodique dans le temps du signal issu des photorécepteurs, appelée encore échantillonnage) doit être suffisamment rapide. La fréquence d'échantillonnage
Facq doit être : Facq
=1/10-8 = 108 Hz =
100
MHz.
Les molécules de silice du coeur de la fibre possède plusieurs niveau d'énergie. On note E0 le nivau fondamental et E1 un niveau excité ( l'étude se limitera à un seul niveau excité). Un photon de l'impulsion laser incidente peut réagir de deux manière avec les molécules de silice : - interaction avec une molécule dans son état fondamental. Le photon, en étant diffusé, cède une partie de son énergie et la molécule passe au niveau excité E1. Le photon repart avec moins d'énergie ( donc avec une fréquence plus faible, avec une longueur d'onde plus grande) ; c'est la raie de Stokes. La conservation de l'énergie conduit à l'énergie du photon rétrodiffusé : E0+hnincident = E1 + hnstokes ; nstokes = nincident + (E0-E1 ) / h avec E0-E1 <0 ; nstokes = c/lincident + (E0-E1 ) / h - interaction avec une molécule dans l'état excité E1. Le photon, en étant diffusé, gagne l'énergie cédée par la molécule qui revient au niveau fondamental E0. Le photon repart avec plus d'énergie ( donc avec une fréquence plus grande, avec une longueur d'onde plus petite) ; c'est la raie de anti-Stokes. La conservation de l'énergie conduit à l'énergie du photon rétrodiffusé : E1+hnincident = E0 + hnanti-stokes ; nanti-stokes = nincident + (E1-E0 ) / h ; nanti-stokes = c/lincident + (E1-E0 ) / h. On note DE = E1-E0 avec DE <<hnincident ; DE << h c /lincident. nstokes =c/lstokes = c/lincident - DE / h ; 1/lstokes = 1/lincident - DE / (hc) =1/lincident[ 1-DE lincident / (hc)]
nanti-stokes =c/lanti-stokes = c/lincident + DE / h ; 1/lanti-stokes = 1/lincident + DE / (hc) =1/lincident[ 1+DE lincident / (hc)]
On montre que : Idiffusée = K Ndépart / l4. A la température T (exprimée en kelvin), la répartition entre les différents niveaux d'énergie est régie par la loi de Boltzmann : le nombre de molécules ayant une énergie E est proportionnel à exp(-E/(kBT). Rapport des intensités des deux raies. I stokes = K N0 / l4stokes ; I anti stokes = K N1 / l4anti stokes ;
I anti stokes / I stokes conduit
à la température. Aucun autre paramètre
physique n'intervient, le système ne subit donc
aucune dérive.
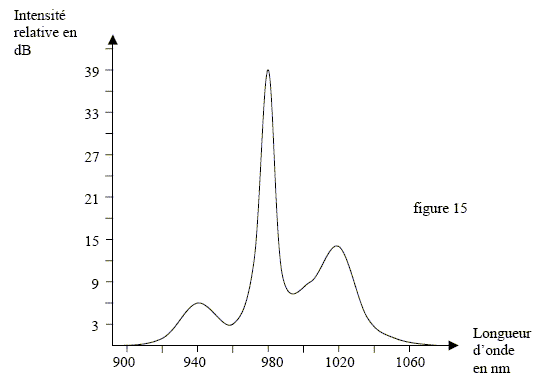
On donne le spectre de la lumière rétrodiffusée par la fibre optique :
Un écart de 2 dB correspond à un rapport d'intensité entre deux raies égal à 100,2 ~1,6. la largeur des raies latérales est dues à l''existence pour les molécules de silice d'une multitude d'états excités. On considèrera la longueur d'onde pour laquelle l'amplitude est maximale. Les trois raies visibles correspondent dand l'ordre : 940 nm , anti-Stokes ; lincident =980 nm, diffusion Rayléigh ; 1020 nm, raie de Stokes. c/lstokes = c/lincident - DE / h ; DE = hc( 1/lincident -1/lstokes ) DE = 6,67 10-34*3 108 [ 1/ 980-1/1020] 109 =7,9 10-21 J. Rapport entre l'intensité de la raie principale et l'intensité de la raie de Stockes : écart des hauteurs : 39-14 = 25 dB soit environ un rapport d'intensité de 1,612,5 = 360. Température à laquelle le spectre a été réalisé : écart des hauteurs entre la raie de Stockes et la raoe anti-Stockes : 14-6 = 8 dB soit environ un rapport d'intensité de 1,64 = 6,5.
l4stokes / l4anti stokes = (1020/980)4 =1,17. exp(E1 / kBT) / exp(E0 / kBT) = exp(DE / kBT) ; DE / kB =7,9 10-21 /1,38 10-23 =572,4 0,15 = 1,17 exp (-572,4/T) ; ln(0,15/1,17) = -572,4/T ; T
= 278 K ( 5°C).
|
||||||||||||||||||||||||||||
|
|