pic d'absorption de l'ion HO- : oscillateur mécanique : concours général 2006

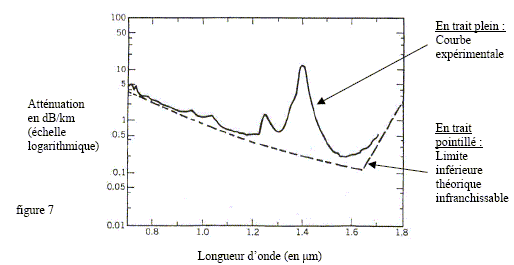
L'atténuation dans une fibre optique dépend de la longueur d'onde l ( par l'intermédiaire du terme s ). On recherche des longueurs d'onde qui subissent l' atténuation la plus faible. Même en absence d'impureté, l'atténuation n'est pas nulle. Une des causes est la diffusion Rayleig : tout atome diffuse nécessairement la lumière. On montre que la puissance diffusée est proportionnelle à 1 / l 4. La diffusion Rayleig incite t-elle à travailler dans l'ultra-violet (UV), le visible ou l'infrarouge ( IR) ? Les longueurs d'onde de l'infrarouge sont supérieures à celle du visible et de l'UV) : dans l'IR la puissance diffusée sera plus faible que dans le visible ou l'UV. La figure suivante représente l'atténuation endB/km dans les fibres optiques en verre en fonction de la longueur d'onde. Si vous aviez à utiliser une fenètre spectrale ( intervalle de longueur d'onde) de 0,1µm pour les télécommunications optiques, laquelle choisiriez-vous ? Dans quel domaine optique se trouve t-on ? L'atténuation doit être la plus faible possible : la courbe présente un minimum vers 1,6 µm ; cette valeur est supérieure à 0,8 µm : elle appartient à l'IR. Le pic principal de la figure est dû à la présence dans la silice d'impuretés que sont les ions HO-. Donner la fréquence ( en THz ; 1 THz = 1012 Hz) correspondant à l'atténuation maximale. l ~ 1,4µ m = 1,4 10-6 m fréquence = vitesse de la lumière / longueur d'onde. fréquence = 3 108 / 1,4 10-6 = 2,1 1014 Hz ~ 2,1 102 THz. 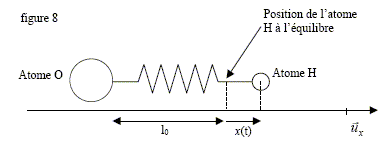Etude du pic d'absorption. On propose un modèle simple expliquant le pic d'absorption. Bien que HO- soit intégré à l'intérieur de la silice, on suppose que les atomes O et H, de masses respectives M et m , sont seuls et ne subissent aucune force extérieure. On raisonne dans le réfréentiel galiléen où le centre de gravité du système constitué par les deux atomes est fixe. On modèlise l'interaction entre les deux atomes par un ressort les liant, de longueur à vide l0 et de raideur k. On ne tient pas compte de la pesanteur. On note ux le vecteur unitaire parallèle à l'axe du ressort dirigé de l'atome d'oxygène vers l'atome d'hydrogène. Donner l'unité de k. N m-1. Expliquer qualitativement pourquoi l'on peut considérer que l'atome d'oxygène reste fixe et que seul l'atome d'hydrogène est en mouvement. La masse M de l'atome d'oxygène est égale à 16 fois la masse m de l'atome d'hydrogène. L'atome d'oxygène est pratiquement au centre de gravité du système constitué par les deux atomes. Or le centre de gravité est fixe dans le référentiel choisi. On repère la position de l'atome H à un instant quelconque ( hors équilibre) par l'abscisse x(t), l'origine du repère étant la position d'équilibre. Etablir l'équation différentielle vérifiée par x(t). 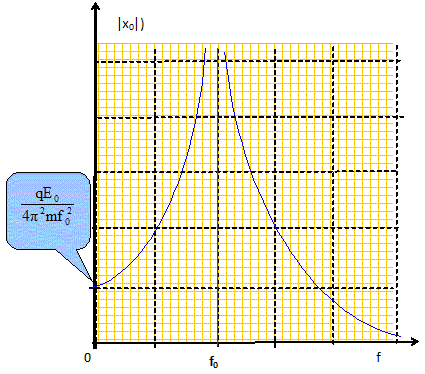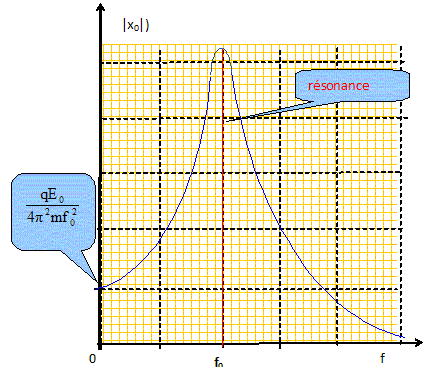Les vecteurs sont écrits en rouge et en gras. L'atome d'hydrogène est soumis à une force de rappel de la forme : kx(t) ( - ux) La seconde loi de Newton s'écrit ( projection sur l'axe Ox) : m d2x/dt2 = - kx d2x/dt2 + k/m x = 0; on pose w20 = k/m. Solution de l'équation différentielle : x(t) = A cos (w0 t+ F) avec A et F sont des constantes. fréquence propre de l'oscillateur : f0 = w0 / (2p) = 1/ (2p) (k/m)½. La différence d'électronégativité entre les atomes d'oxygène et d'hydrogène entraîne l'apparition d'une charge électrique q au voisinage de l'atome d'hydrogène. Or la lumière est une onde électromagnétique et possède un champ électrique oscillant E(t). Ainsi la lumière guidée dans la fibre optique arrivant sur un ion HO- va mettre en mouvement l'atome d'hydrogène. Pour une lumière monochromatique de fréquence f, on admet que le champ électrique associé à l'onde luminsuse s'écrit : E(t) = E0 cos ( 2pf t) ux, où E0 est une constante. L'atome H subit la force supplémentaire F = qE. Etablir la nouvelle équation différentielle vérifiée par x(t). L'atome d'hydrogène étant moins électronégatif que l'atome d'oxygène, la charge q est positive et F est colinéaire et de même sens que E. La seconde loi de Newton s'écrit ( projection sur l'axe Ox) : m d2x/dt2 = - kx +qE0 cos ( 2pf t) d2x/dt2 + k/m x = q / m E0 cos ( 2pf t). (1) On cherche la solution particulière sous la forme x(t) = x0 cos ( 2pf t) : l'atome d'hydrogène oscille à la fréquence f avec une amplitude |x0|. Déterminer la constante x0 . Dériver deux fois x(t) = x0 cos ( 2pf t) par rapport au temps : x'(t) = -x0 2pf sin ( 2pf t) ;x"(t) = -x0 (2pf )2 cos ( 2pf t) ; repport dans (1) : -x0 (2pf )2 cos ( 2pf t) +k/m x0 cos ( 2pf t) = q / m E0 cos ( 2pf t). x0 ( k/m -(2pf )2 = q / m E0 ; or w20 = (2pf0 )2 = k/m ; 4p2x0 ( f02 -f 2) = q / m E0 ; x0 = qE0 m 4p2 ( f02 -f 2) Donner l'allure du graphe représentant l'amplitude |x0| en fonction de la fréquence f. Que se passe t-il pour f=f0 ? Que manque t-il au modèle pour correspondre mieux à la réalité ? L'amplitude tend vers l'infini ( cela n'est pas réaliste) ; il manque à ce modèle des forces dissipatives d'énergie : l'atome pers de l'énergie par rayonnement). Dessiner l'allure du graphe |x0| en fonction de la fréquence dans ce cas. Comment se nomme le phénomène qui a lieu autour de la fréquence f0 ?   Le grand pic d'absorption de la figure correspond en fait à la première harmonique de l'oscillation de la liaison H--O, c'est à dire que la fréquence du pic vaut le double de la fréquence propre de la liaison. Calculer la masse ( en kg) d'un atome d'hydrogène et en déduire la valeur numérique de la raideur du ressort utilisé dans ce modèle. masse d'un atome = masse molaire / nombre d'Avogadro = 10-3 / 6 1023 = 1,7 10-27 kg. 2f0 =214 THz ; f0 =107 THz = 1,07 1014 Hz. f0 = 1/ (2p) (k/m)½ ; k = f02 *4p2 m k = 1,072 1028*4*3,142* 1,7 10-27 =7,7 102 N m-1. i

retour -menu