Propagation de la lumière dans les fibres optiques : concours général 2006

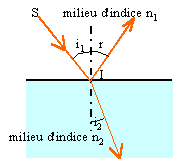
Le phénomène de réflexion totale : Que signifie le terme "lumière monochromatique" en optique. Une seule couleur, une seule fréquence. Dans toute la suite, les rayons lumineux sont tous supposés issus d'une radiation monochromatique. On considère un rayon lumineux arrivant sur l'interface plane séparant deux milieux d'indice différents ( notés n1 et n2) sous un angle d'incidence i1 par rapport à la normale à l'interface. 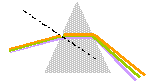Lois de Descartes relatives à la réflexion et à la réfraction de la lumière : Les trois rayons incident, réfléchi et réfracté sont dans le même plan ; l'angle d'incidence i1 est égal à l'angle de réflexion r. Les angles d'incidence i1 et réfracté i2 sont reliés par la relation : n1 sin i1 = n2 sin i2. Citer et décrire une expérience montrant la dépendance de l'indice du verre par rapport à la longueur d'onde. Dispersion de la lumière par un prisme : après avoir traversé le prisme de verre, les différentes radiations colorées constituant la lumière blanche sont déviées différemment ; dans le prisme les vitesses de propagation sont différnetes pour des radiations de fréquences différentes. Le bleu est le plus dévié. On suppose que n1 > n2. Montrer que si i1>i0 aucun rayon réfracté ne peut émerger. n1 sin i1 = n2 sin i2 ; sin i2 = n1 / n2 sin i1. La valeur maximale de i2 est 90° soit sin i2 = 1 d'où sin i0 = n2/n1. Dans la situation i1 > i0 on dit que le rayon incident subit une réflexion totale. Calculer la valeur de 90-i0 si n1 = 1,500 et n2 = 1,470. sin i0 = n2/n1 = 1,470/1,500 =0,980 ; i0 =78,52° ; 90-i0 = 11,48°. 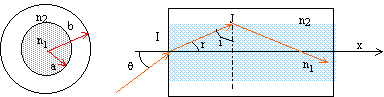Fibre à saut d'indice : Une fibre optique est constituée d'un coeur cylindrique transparent d'indice n1=1,500 entourée d'une gaine transparente d'indice n2 = 1,470. L'axe de la fibre est normal au dioptre air/coeur. Un rayon laser se propageant dans l'air dans un plan contenant l'axe de la fibre pénètre dans le coeur de la fibre. Le rayon incident au point I reste dans le coeur si l'angle qi d'incidence à l'entrée de la fibre est inférieur à un angle a que l'on va calculer : en I, dioptre air/coeur : nair sin qi = n1 sin r ; sin qi = n1 sin r (1) en J, il y a réflexion totale : dioptre coeur/gaine : n1 sin i = n2 sin 90 = n2 ; sin i = n2 /n1 = 1,470 / 1,500 = 0,98 ; i = 78,52° ; les angle i et r sont complémentaires soit : sin r = cos i = cos 78,52 = 0,199 de plus (1) s'écrit : sin a = n1 sin r = 1,5*0,199 =0,298 ; a = 17,4°. Expression de l'ouverture numérique ON = sin a en fonction de n1 et n2. (1) s'écrit : sin a = n1 sin r ; en J, il y a réflexion totale : sin i = n2 /n1 et sin r = cos i. sin2 i = (n2 /n1)2 ; cos2 i =1-sin2 i =1-(n2 /n1)2 = (n12-n22) / n12. cos i =sin r = (n12-n22)½ / n1 ; or sin a = n1 sin r = (n12-n22)½. Exprimer la vitesse de propagation de la lumière dans le coeur de la fibre en fonction de n1 et c, vitesse de la lumière dans le vide. 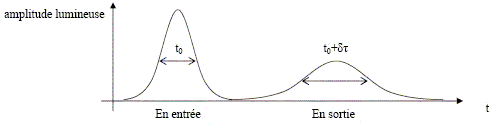v = c/n1. On considère une fibre optique de longueur L. Le rayon entre dans la fibre avec un angle d'incidence q variable entre 0 et a. Quel est le rayon qui traverse le plus rapidement la fibre ? Calculer la durée t1 du parcours de ce rayon. Quel est le rayon qui met le plus de temps pour traverser la fibre ? Calculer la durée t2 du parcours de ce rayon en fonction de L, c, n1 et sin a. Expression de la distance d parcourue par la lumière en fonction de son angle d'incidence qi et de la longueur de la fibre L : si l'angle d'incidence q =0, le rayon parcourt la distance L en t1 seconde, à la vitesse v = c/n1. t1 = L/v = L n1 / c. si l'angle d'incidence q =a, le rayon parcourt la distance d =n fois IJ, en t2 seconde, à la vitesse v = c/n1. Figure ci-dessus, expression de IJ : ( on note h la projection de IJ sur l'axe de la fibre) cos r = h / IJ; or sin qi = n1 sin r ; cos² r + sin² r = 1 ; h²/IJ² +( sin qi / n1 )² = 1 ; h / IJ = [1-( sin qi / n1 )² ]½. Le rapport entre la longueur L de la fibre et le trajet d suivi par la lumière est : L/d =[1-( sin qi / n1 )² ]½ d = L[1-( sin qi / n1 )² ]-½ soit d = L[1-( sin a / n1 )² ]-½ t2 =d/v = L/ v [1-( sin a / n1 )² ]-½ = L n1 / c [1-( sin a / n1 )² ]-½ . En déduire l'intervalle de temps dt =t2 -t1 en fonction de L, c, n1 et n2. dt = L n1 / c [1-( sin a / n1 )² ]-½ - L n1 / c = L n1 / c [ [1-( sin a / n1 )² ]-½ -1] avec sin² a = n12-n22 d'où [1-( sin a / n1 )² ]-½ = n1 / n2 ; dt =L n1 / c [ n1 / n2 -1]. On pose 2D= 1 -(n2 /n1)2. Montrer que si D<<1, dt ~Ln1D / c. (n2 /n1)2 = 1-2D ; n2 /n1= (1-2D)½ ; n1 /n2= (1-2D)-½ ~ 1+D si D <<1. n1 /n2-1 = D d'où : dt ~Ln1D / c. L'impulsion lumineuse s'étale dans la fibre : les différents rayons dans la fibre ne mettent pas le même temps pour la traverser. La durée de l'impulsion de sortie est l'écart temporel entre le rayon le plus rapide émis au début de l'impulsion et le rayon le plus lent émis à la fin de l'impulsion ; la durée de l'impulsion de sortie est de l'ordre de t0+dt. L'amplitude de l'impulsion diminuer du fait de son étalement ( conservation de l'énergie lumineuse transportée). Le codage binaire de l'information consiste à envoyer des impulsions lumineuses " bits" périodiquement avec une fréquence d'émission F. En supposant t0 négligeable devant dt, quelle condition portant sur la fréquence F exprime le non recouvrement des impulsions de sortie. Durée entre chaque impulsion T = 1/F ; il y a non recouvrement à la sortie si dt < T. Soit Lmax la longueur maximale de la fibre optique permetttant d'éviter le phénomène de recouvrement d'impulsion. On appelle bande passante de la fibre le produit B= Lmax F. Exprimer la bande passante en fonction de D, n1 et c. à la limite du recouvrement : T = 1/F =dt ~ Lmax n1D / c. B= LmaxF = c / (n1D ). La bande passante est la longueur maximale au delà de laquelle il est impossible de transmettre. A.N : F = 100 MHz = 108 Hz ; n1 = 1,5 , n2 = 1,47. 2D = 1 -(n2 /n1)2 = 1-(1,47/1,5)2 =0,0396 ; D =0,0198. B = c / (n1D ) = 3 108/(0,0198*1,5) =1,01 1010 m s-1. Lmax = B / F = 1,01 1010 / 108 =101 m. Si le rayon de la fibre est trop petit, le modèle de l'optique géométrique utilisé jusqu'à présent, n'est plus valable. Il faut traiter la lumière comme une onde. Indiquer un phénomène relatif à la lumière mettant en évidence son caractère ondulatoire. Diffraction par une fente ou un obstacle dont les dimensions sont de l'ordre de grandeur de la longueur d'onde de la lumière.

retour -menu