Forme de la terre : concours général 2005

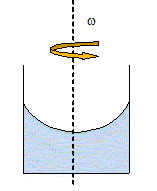
Dès le 18ème siècle, on avait établi expérimentalement que la Terre était aplatie aux pôles. On étudie dans cette partie un modèle qui justifie ce fait expérimental. Illustration qualitative du problème. On verse de l’eau dans un récipient cylindrique dont on maintient l’axe vertical. L’ensemble est au repos, la surface libre est plane et horizontale. 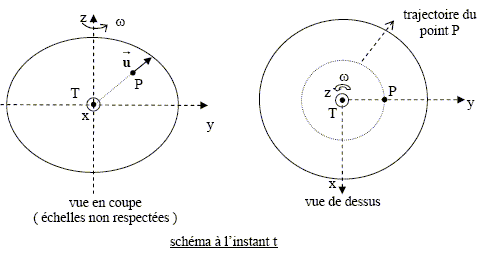On fait tourner à vitesse angulaire constante le récipient autour de son axe vertical ; la nouvelle forme adoptée par cette surface libre au bout de quelques instantsest la suivante : On constate ainsi que la mise en rotation d’un fluide est susceptible de modifier la forme de sa surface libre. La forme du globe terrestre. On se propose dans cette question d’expliquer le fait que la rotation de la Terre sur elle-même a une influence sur sa forme en la renflant à l’équateur. Le référentiel d’étude est le référentiel géocentrique supposé galiléen. On choisit pour repère ( T, x, y, z ). La Terre de masse M et de centre T est supposée bien modélisée par un « fluide » à répartition uniforme de masse et à symétrie de révolution autour de l’axe des pôles Tz. Ce « fluide », qui modélise la Terre, tourne donc en bloc autour de l’axe fixe Tz à la vitesse angulaire w =7,292.10-5 rad.s-1. Les vecteurs sont écrits en gras et en rouge. Pour simplifier, on considère un point P intérieur à la terre situé à l’instant t dans le plan ( Tyz ) ; y et z représentent ainsi ses coordonnées dans ce plan. On pose u = TP /||TP|| et r = ||TP||. On désigne par ( ex, ey, ez) la base orthonormée associée au repère ( T, x, y, z ). Ce point P décrit une trajectoire circulaire et est animé d’un mouvement uniforme de vitesse angulaire w. Expression, à l’instant t, du vecteur vitesse V du point P par rapport au référentiel géocentrique : V = w y (-ex) = -w yex. Expression, à l’instant t, du vecteur accélération a par rapport au référentiel géocentrique. accélération centripète : a = V2/y (-ey) = -w2 y ey. Forces de pression interne. On isole par la pensée un petit élément de volume de masse m situé au voisinage du point P ; cet élément de volume est soumis à l’action de la force de gravitation FG et à la résultante des forces de pression que l’on note FP. On supposera pour cela que la force de gravitation est celle que subirait un point matériel de masse m situé à la surface d’une sphère homogène de rayon r et de même masse volumique moyenne r que celle de la terre. masse de la terre M = 4/3 pR3r ; masse d'une sphère de rayon r, de masse volumique r : m' =4/3 pr3r =Mr3 / R3. FG = G m'm/r2 (-u) = -GM m /R3 r u. Ecrire la seconde loi de Newton appliquée au point P de masse m : FG +FP =-mw2 y ey. FP = -mw2 y ey + GM m /R3 r u. Composantes FPy et FPz du vecteur FP suivant les axes y et z, à l’aide des coordonnées y et z du point P. r u = zez + y ey ; FP = -mw2 y ey + GM m /R3 (zez + y ey) = GM m /R3 zez + (-mw2 y+GM m /R3 y)ey. FPy =-mw2 y+GM m /R3 y ; FPz =GM m /R3 z. La forme de la terre. 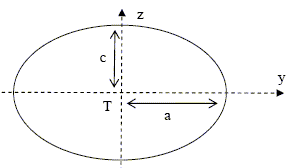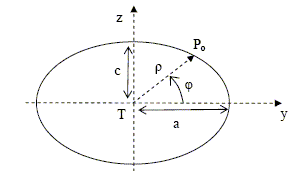On admet que la surface stable du « fluide Terre » est en tout point perpendiculaire à la résultante des forces de pression FP calculée pour un point P situé à la limite de cette surface. L’équation d’une ellipse (aucune connaissance relative à cette famille de courbes n’estnécessaire à la résolution de la suite du problème) est en coordonnées cartésiennes : y2/a2 + z2/c2=1 ; a représente la longueur du demi-grand axe et c celle du demi-petit axe. On admet que dans le plan (Tyz), le vecteur de composantes ( y/a2 ; z/c2 ) est perpendiculaire à l’ellipse définie ci-dessus au point de coordonnées (y,z). Enfin, on montre que l’équation de la trace de la surface de libre du « fluide Terre » dans le plan (Tyz), est celle de l’ellipse définie ci-dessus. Expression du rapport a2/c2 en fonction de G, M, R et w : FP et le vecteur normal à l'ellipse sont colinaires : ( k est une constante) FPy =ky/a2 = -mw2 y+GM m /R3 y ; FPz = k z/c2 =GM m /R3 z ; FPz / FPy = a2 z / (c2 y2) ; a2/ c2 =FPz y / (FPyz) FPz y FPyz = GM (-w2R3 +GM ) = GM / R3 (-w2 +GM /R3) Evaluons le rapport e =w2R3 / (2GM), rapport sans dimension. e = (7,292.10-5)2 *(6,37 106)3 / (2*6,673 10-11 *5,974 1024)=1,72 10-3. Donner une expression approchée du coefficient f= (a-c)/c en fonction de e ; a2 c2 = 1 1-2e ; a c = 1 (1-2e )½ a / c ~ 1+e ; a/c-1 ~e ; f = (a-c)/c ~e. déterminer f numériquement et comparer la valeur obtenue à celle actuellement admise et qui est de l’ordre de 1/298,25. f ~ 1,72 10-3 = 1/ 581, valeur inférieure à la valeur expérimentale. Amélioration du modèle. Un étude plus fine prenant en compte la dépendance de la force de gravitation avec la latitude j du point permet d’établir que l’équation de la surface libre du « fluide Terre » s’écrit : r désigne la distance d’un point P0 de la surface au centre T de la Terre et j la latitude. Expliciter la constante Cste en fonction de e1 et e2. si j = 0 et r = a : a / r +e1a3 / r3 +e2a3 / r3 = Cste 1+ e1 + e2 = Cste. On pose r = a(1+h) où h est une grandeur petite devant 1. Donner une expression approchée de h sous la forme h = -h(e1, e2) sin2j. Expliciter h(e1, e2). a /r = (1+h)-1 ; a /r ~1-h ; a3 / r3 ~1-3h ; r2 /a2 ~ 1+2h. De plus les termes contenant les produits he1 et he2 seront négligeables devant les autres. L'expression ci-dessus s'écrit : 1-h +e1(1-3h)(1-3sin2j) +(1+2h) e2 cos2j = 1+ e1 + e2. -h +e1(1-3sin2j) +e2 cos2j = e1 + e2. -h -3e1sin2j -e2 sin2j = 0 ; h = -(3e1+e2) sin2j. h(e1, e2) = 3e1+e2. Effectuer une nouvelle évaluation numérique du rapport f=(a-c)/c et conclure. f ~3e1+e2 ; e2 = (7,292.10-5)2 *(6,378 106)3 / (2*6,673 10-11 *5,974 1024)=1,73 10-3. f ~ 3*5,4 10-4 +1,73 10-3 =3,35 10-3 = 1 / 298,5, très proche de la valeur expérimentale.

retour -menu