Détection des cavités et hétérogénéités dans le sous-sol : concours général 2005

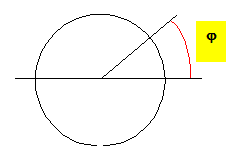
Pour pouvoir aborder la notion d’anomalie gravimétrique, il nous faut introduire la notion d’ellipsoïde de référence. L’ellipsoïde de référence est une surface qui épouse au mieux la forme de notre planète indépendamment des accidents topographiques. C’est une surface de révolution qui se nomme GRS-80 et dont la définition a été stabilisée dans les années 1980. Sur l’ellipsoïde de référence on peut déterminer une valeur de référence gref de l’intensité du champ de pesanteur. Cette valeur de référence dépend de la latitude j du point considéré et vaut : gref = 978031 (1+0,005302357 sin2j -0,000005865 sin2(2j)). 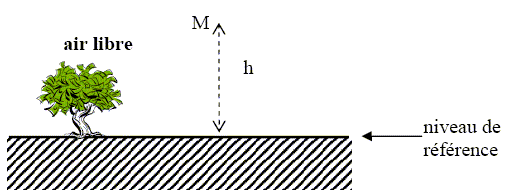La latitude ne suffit pas à définir de façon unique la position d'un point à la surface de la terre. si j=0, gref = 9,78 m s-2,valeur à l'équateur ; si j=90, gref = 9,83 m s-2,valeur aux pôles. Corrections gravimétriques. On se propose d’étudier le champ de pesanteur en un point situé à une altitude h. Deux cas sont envisagés : l’espace entre le niveau de référence et le point M est constitué par de l’air, on parle alors de « correction à l’air libre » ; cet espace est occupé par un plateau, il s’agit de « correction de plateau » Correction à l’air libre. Un point M est situé à une altitude h. L’espace compris entre le niveau de référence et ce point est occupé par de l’air. On suppose que h << R et on peut se référer à la figure : Variation de g en fonction de h : g = GM / (R+h)2. g diminue si l'altitude h augmente. g0 = GM / R2 ; g = GM / [ R2 (1+h/R)2] = g0 / (1+h/R)2 ~g0 (1-2h/R) g-g0 = -2hg0/R. AN : h = 1038 m ; g-g0 = -2*1038*9,8/6,378 106 =-3,2 10-3 ms-2 =-3,2 10-1 Gal = -320 mG. Lorsque la hauteur h varie de Dh en valeur absolue, g varie de Dg en valeur absolue. Avec les instruments modernes, la précision expérimentale sur la mesure de D g est de l'ordre de 5 µGal = 5 10-8 m s-2, estimer la plus petite valeur de Dh mesurable et commenter ce résultat. Dg = -2g0Dh/R ; Dh = 0,5 R Dg /g0 = 0,5*6,378 106 *5 10-8 /9,8= 1,6 cm. La rigueur est de mise dans le déroulement des mesures. Correction de plateau. 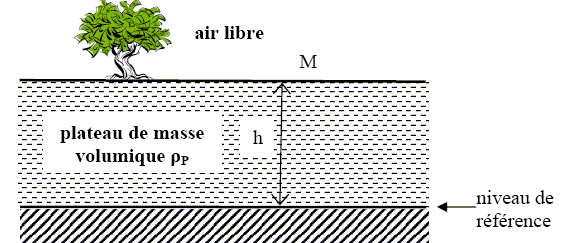L’espace entre le niveau de référence et M est à présent occupé par un « plateau » de masse volumique rP. On admet que l’intensité du champ de gravitation supplémentaire créé au point M par le plateau est donnée par l’expression : 2pGrPh. Montrons que 2pGrPh a les dimensions d'une accélération. G : m3 kg-1 s-2 ; rP : kg m-3 ; h : m ; 2p sans dimension. 2pGrPh : m s-2. La correction de plateau est proportionnelle à la hauteur h ; l’intensité du champ de gravitation augmente avec h. Calculons cette correction en mGal pour h = 1038 m et rP=2,80 103 kg m-3 : 2pGrPh = 2*3,14*6,673 10-11*2,80 103 *1038 =1,22 10-3 m s-2 = 0,122 gal = 122 mGal. Expression littérale de la différence g0 - g qui prend en compte les deux effets : correction d’air libre et correction de plateau. g- g0 = 2pGrPh -2hg0/R. si h = 1038 m et rP=2,80 103 kg m-3 : g- g0 =-320 +122 = -198 mGal. Anomalies gravimétriques. L’anomalie gravimétrique, notée AB, ou anomalie de Bouguer (en hommage au savant français Pierre Bouguer) est la différence entre la valeur mesurée, notée gmes, et la valeur de référence corrigée des corrections d’air libre et de plateau, notée gc. AB = gmes-gc. Elle nous donne des informations sur les hétérogénéités de la répartition des masses internes au globe terrestre. Détection d'une cavité. On suppose qu’une cavité de forme sphérique de rayon R = 5 m et située à une profondeur H = 20 m, est présente dans le plateau de masse volumique rP=2,80 103 kg m-3 .Le centre de la cavité a pour abscisse x0 suivant un axe horizontal Ox. On procède à une mesure de l’intensité du champ de pesanteur le long de l’axe Ox. En absence de cavité l’anomalie gravimétrique AB est nulle. En présence de la cavité, on observe une diminution de la valeur de gc ( dû au défaut de masse). Expression littérale de la valeur maximale ABmax de AB : volume de la sphère de rayon r : V = 4/3 p r3 ; masse correspondante : m = 4/3 p rP r3 ; Au champ de gravitation on retranche la contribution de cette masse manquante : ABmax = - 4/3G p rP r3 /H2. Détection d’un dôme de sel au Texas. 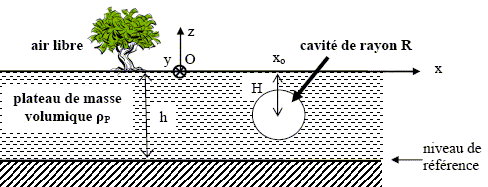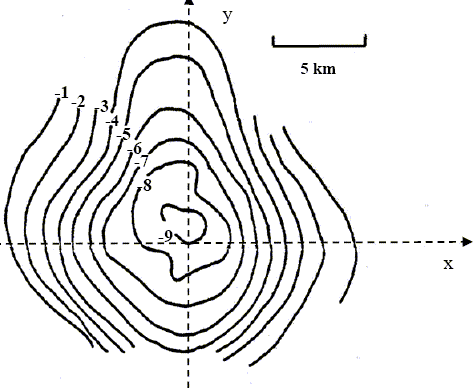La figure ci-dessous propose un profil d’anomalie gravimétrique effectué selon le principe précédent mais pour le plan horizontal xOy. On y représente les courbes de niveau pour différentes valeurs de AB exprimées en mGal. On suppose que le sel a pour masse volumique r=2,2 103 kg m-3 et que la masse volumique moyenne des sédiments est rP=2,4 103 kg m-3. Le dôme de sel, de forme sphérique, est situé à une profondeur H de l’ordre de 6 km et possède un rayon r de l’ordre de 4 km. L’anomalie gravimétrique observée sur le dôme de sel est négative, car la masse volumique du sel est inférieure à celle des sédiments. AB = - 4/3G p Dr r3 /H2 = -4/3*6,673 10-11*0,2 103 * (4 103)3 / (6 103)2 = -10-6 Gal = - 10µGal.

retour -menu