Le champ de pesanteur terrestre : concours général 2005

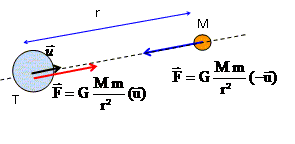
la terre de masse M et de centre T est supposée modélisée par une répartition de msse à symétrie sphérique de rayon R. Un point matériel de masse m est placé en un point M situé à une distance r >R du centre T de la terre. On note G la constante de gravitation. 1ère étude : Isaac Newton ( 1642 - 1727 ) énonce la loi de la gravitation. 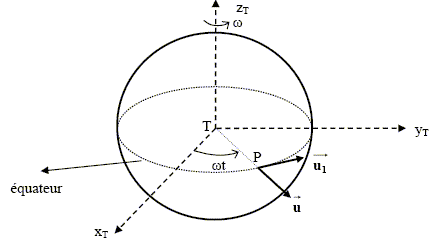Force d'interaction gravitationnelle exercée par la terre sur un point matériel de masse m situé à la distance r : R = 6370 km = 6,370 106 m ; M = 5,974 1024 kg ; G = 6,673 10-11 m3 kg-1 s-2. Valeur g0 de l'intensité de la pesanteur à la surface de la terre : g0 = GM/R2 =6,673 10-11 *5,974 1024 /(6,370 106)2 = 9,824 m s-2. Etude plus précise : Le référentiel d'étude est le référentiel géocentrique supposé galiléen. On choisit pour repère (T, xT, yT, zT). La terre est animée d'un mouvement de rotation autour de l'axe fixe TzT à la vitesse angulaire w. On donne TS =86164 s, le jour sidéral. w = 2p / TS = 6,28 / 86164 =7,292 10-5 rad/s. Le point P du plan équatorial décrit une trajectoire circulaire et est animé d'un mouvement uniforme. Un vecteur est écrit en gras et en rouge. Vitesse V du point P par rapport au référentiel géocentrique : V =wR u1. Valeur ( norme) V = 7,292 10-5 *6,370 106 =464,5 m /s. Accélération a du point P par rapport au référentiel géocentrique : a =V2 /R (-u) =w2R(-u) Valeur ( norme) a = 464,52 / 6,370 106 =3,387 10-2 m s-2. Le point P représente maintenant un point matériel de masse m suspendu par un fil au voisinage immédiat de la surface de la terre. Situé au niveau de l'équateur, il est immoile par rapport à la surface de la terre donc est animé, par rapport au référentiel géocentrique, du mouvement circulaire uniforme étudié ci-dessus. Sur la figure suivante, les échelles ne sont pas respectées. 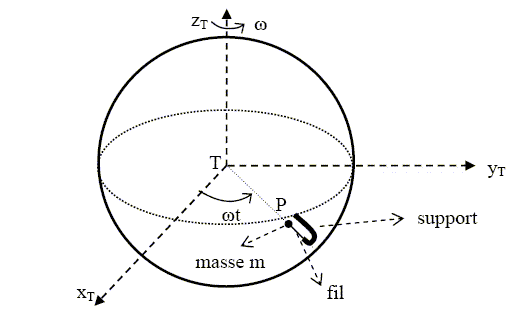Dans un référentiel galiléen, la première loi de Newton ( principe d'inertie) est vérifiée. Forces exercée sur le point matériel P : - T0 exercée par le fil ; - force attractive de la terre notée F. Appliquons la seconde loi de Newton à P : T0 + F = m a = mw2R(-u) La mesure expérimentale du poids d'un corps peut être faite de la manière suivante : suspendre le corps à un dynamomètre ; à l'équilibre, la valeur donnée par le dynamomètre est égale au poids. On définit le poids par : P = -T0 = F + mw2R u. P = GMm/R2 (-u) - mw2R (-u) et en divisant par m : g = (GM/R2 - w2R) (-u) valeur g = 9,824 -(7,292 10-5 )2*6,370 106 =9,790 m s-2. La terre est une sphère applatie aux pôles ; distance du centre de la terre au pôle ; RP = 6357 km valeur gpôle =6,673 10-11 *5,974 1024 /(6,370 106)2 -(7,292 10-5 )2*6,357 106 =9,83 m s-2. Rayon à l'équateur : RP = 6378 km valeur géquateur =6,673 10-11 *5,974 1024 /(6,378 106)2 -(7,292 10-5 )2*6,378 106 =9,78 m s-2. Influence de la Lune et du Soleil. 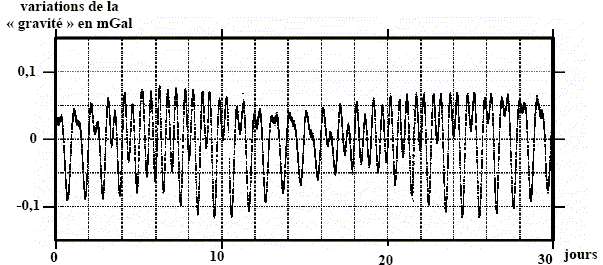Une masse ponctuelle située à la surface du globe terrestre subit également l’attraction des corps massifs externes en particulier de la Lune et du Soleil. L’intensité du champ de pesanteur varie donc au cours du temps en faisant apparaître des durées typiques reliées aux différentes périodes associées à la rotation de la Terre sur elle-même, au mouvement de rotation de la Lune autour de la Terre et à celui de la Terre autour du Soleil. Ces variations temporelles de g, intensité du champ de pesanteur, font l’objet de mesures très précises à l’aide de « gravimètres ». La figure ci-dessous montre des mesures de celles-ci en région parisienne. L’unité de mesure est le mGal où le Gal est une unité utilisée par les géophysiciens 1 Gal = 10-2 m s-2. On distingue des phénomènes périodiques de période proche de 12 h et de période proche de 30 jours ( une lunaison). Un modèle simplifié établit que l’amplitude des variations de l’intensité du champ de pesanteur terrestre dues à un astre A s’écrit : 2GMA R/ DA3 : MA est la masse de l’astre et DA sa distance au centre de la Terre. Evaluons cette amplitude de variation dans le cas de la Lune de masse ML = 7,3.1022 kg et située à la distance DL = 3,8.108 m de la Terre. 2GML R/ DL3 =2*6,673 10-11 *7,3.1022 *6,378 106/(3,8.108)3=1,13 10-6 m s-2. soit 1,13 10-4 Gal = 0,11 mGal, valeur comparable l'amplitude lue sur de la figure ci-dessus. Evaluons de même celle-ci dans le cas du Soleil de masse MS = 2,0.1030 kg et situé à la distance DS = 1,5.1011 m de la Terre. 2GMS R/ DS3 =2*6,673 10-11 *2,0.1030 *6,378 106/(1,5.1011)3=5,0 10-7 m s-2. soit 5,0 10-5 Gal = 0,05 mGal. L’influence de la Lune est le double de celle du Soleil.

retour -menu