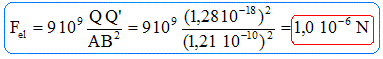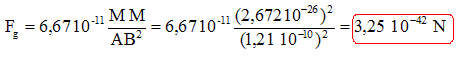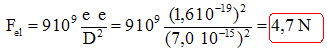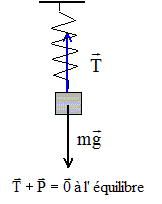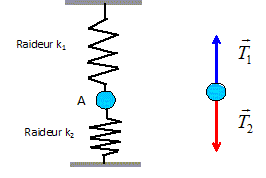
Interractions dans la molécule de dioxygène ; équilibre avec des ressorts.

Dans la molécule de dioxygène O2, les deux atomes d'oxygène sont distants de 121 pm = 121 10-12 m = 1,21 10-10 m. Le noyau d'unn atome d'oxygène compte 8 neutrons et 8 protons. Le nombre de charge, noté Z, d'un atome d' oxygène est égal au nombre de protons : Z = 8. Le nombre de masse, noté A, de cet atome est égal aux nombre de nucléons ( protons + neutrons ) : A = 8+8 = 16. La charge électrique, notée Q, d'un noyau est égale à 8 fois la charge d'un proton : Q = 8 e e : charge élémentaire ; e = 1,6 10-19 C. Q = 8 * 1,6 10-19 = 1,28 10-18 ~1,3 10-18 C. La masse, notée M, d'un noyau est égale à la masse des nucléons ; la masse d'un nucléon est m = 1,67 10-27 kg. M = 16 *1,67 10-27 =2,672 10-26 ~ 2,67 10-26 kg. Force électrique ( ou forces de Coulomb) s'exerçant entre ces deux noyaux chargés positivement. Les deux noyaux chargés positivement se repoussent. La valeur de la force de répulsion est égale à : Force de gravitation s'exerçant entre ces deux noyaux de masse M. Les forces de gravitation sont toujours attractives. La valeur de cette force est égale à : Le diamètre du noyau d'un atome d'oxygène est de l'ordre de D = 7,0 10-15 m. On considère deux protons de ce noyau distants de D. Force électrique ( ou forces de Coulomb) s'exerçant entre ces deux protons chargés positivement. Les deux protons chargés positivement se repoussent. La valeur de la force de répulsion est égale à : Force de gravitation s'exerçant entre ces deux protons de masse m. Les forces de gravitation sont toujours attractives. La valeur de cette force est égale à :   La force électrique est bien supérieure à la valeur de la force de gravitation. Si les protons n'étaient soumis qu'à ces deux forces, les protons se repousseraient et ne pourraient rester dans le noyau de l'atome. Or le noyau de l'atome d'oxygène est stable : il faut donc prendre en compte une autre force. L'interaction "forte" assure la cohésion des noyaux ; cette interaction n'agit que sur de très courtes distances.       Equilibre avec des ressorts. L'extrémité inférieure du ressort est soumise à : l'action de la masse, verticale vers le bas, valeur P=mg ( masse en kg) à la tension du ressort, verticale vers le haut, valeur T= k x ( k : raideur en N/kg et x : allongement en m) T= mg = kx On donne k = 25 N/m ; m = 80 g = 8,0 10-2 kg ; g = 10 N / kg. L'allongement x du ressort vaut : x = mg / k = 8,0 10-2 * 10 / 25 =0,032 m = 3,2 cm.       Le petit disque A a une masse négligeable. Les deux ressorts sont étirés. Le système est à l'équilibre. L'allongement du ressort du bas est x2=1,5 cm ; l'allongement du ressort du haut est noté x1. On donne k1 = 25 N/m, k2 = 60 N/m. Le petit disque A est à l'équilibre sous l'action des tensions des deux ressorts : T1 : verticale, vers le haut, valeur : k1 x1 ; T2 : verticale, vers le bas, valeur : k2 x2. Le principe d'inertie condduit à : T1 = T2 ; k1 x1 = k2 x2. x1 = k2 x2 / k1 =60*1,5 / 25 =3,6 cm.

retour -menu