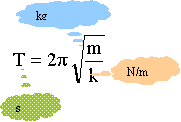Energie mécanique : bille de flipper

Un ressort de masse négligeable, à spires non jointives, a un coefficient de raideur k et une longueur vide l0. L'axe du ressort est horizontal. Il est fixé à son extrémité gauche à un support fixe. Une bille, de masse m = 150 g, est fixée à son extrémité droite. Le mouvement de la bille est étudié dans le repère (O, i). L'origine O du repère coincide avec la position de repos du centre d'inertie de la bille (le ressort étant ni étiré ni comprimé) : l'axe est orienté de la gauche vers la droite. On comprime le ressort de sorte qu'à l'instant initial t = 0, x(0) = -0,10 m, puis on abandonne la bille sans vitesse initiale. On chronomètre 15 oscillations de la bille pendant lesquelles l'amplitude ne varie pas notablement : on lit une durée de 6,12 s. Déterminer T0 . T0 = 6,12 / 15 = 0,408 s ~ 0,41 s. Exprimer la constante de raideur k en fonction de m et de T0 puis la calculer. T02 = 4 p2 m/k ; k = 4 p2 m/T02 ; k = 4*3,142*0,15 / 0,4082 =35,57 ~ 35,6 N /m. Dans la suite du problème, on utilise ce ressort comme lanceur de bille d'un flipper. Dans cette partie, la bille est (S) est libre et n'est donc plus solidaire de l'extrémité du ressort. Le flipper est constitué d'un plan horizontal et d'un plan incliné d'un angle (ß = 20° sur l'horizontale et d'une longueur L = 80 cm. Au sommet du plan incliné se trouve la cible H à atteindre. On pose la bille (S) contre le ressort et on le comprime de 5 cm. Une fois le système libéré, la bille quitte le ressort et poursuit son mouvement en glissant sans frottement sur la portion de plan horizontal puis sur le plan incliné avant d'atteindre la cible H. D'où provient l'énergie cinétique acquise par la bille ? Système {bille ressort} ; conservation de l'énergie mécanique en absence de frottement. Le ressort comprimé possède de l'énergie potentielle élastique ½k a2 avec a = 0,05 m. Celle-ci est transférée à la bille sous forme d'énergie cinétique sur le plan horizontal. On suppose que la bille quitte le ressort quand celui-ci reprend sa longueur à vide l0. Etablir alors l'expression littérale de la vitesse v0 avec laquelle la bille quitte le ressort puis effectuer l'application numérique. Conservation de l'énergie mécanique : ½k a2 = ½mv02. v02 = k a2 / m ; v0 = a (k/m)½ =0,05 (35,57/0,15)½ =0,77 m/s. Quelle est la vitesse de la bille en A, en bas du plan incliné ?  Sur la partie horizontale la bille est soumise à son poids et à l'action du plan ; ces deux forces perpendiculaires à la vitesse, ne travaillent pas. L'énergie cinétique, donc la vitesse de la bille ne varient pas et vA = 0,77 m/s. Quelle vitesse minimale, Vmin , doit posséder la bille, en A, pour atteindre la cible H ? 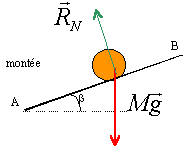Sur le plan incliné la bille est soumise à l'action du plan (perpendiculaire au plan si pas de frottement) et à son poids : Travail résistant du poids au cours du déplacement AH = L : mg(hA-hH) avec HA = 0 origine des altitudes et HB = Lsinb = 0,80 sin 20 = 0,294 m W(poids) A-->B = -mgLsinb L'action du plan perpendiculaire au plan ne travaille pas. Variation d'énergie cinétique = travail du poids DEc = ½mv²H - ½mv²A = -mgLsinb. 0 - ½mv²mini = -mgLsinb. v²mini =2gL sin ß ; vmini = (2gL sin ß)½. vmini =(2*9,8*0,8*sin20)½= 2,316 ~ 2,32 m/s. En utilisant les résultats des questions précédentes, établir l'expression littérale de X0 min de compression initiale du ressort pour que la bille atteigne la cible H. Faire ensuite l'application numérique. Energie potentielle élastique initiale du système { bille -resort} : ½kX20 min Energie cinétique du système (bille en mouvement, ressort non déformé ) en A : ½m v2 min Energie potentielle de pesanteur du système (bille à l'arrêt, ressort non déformé ) en H : mgLsin ß Conservation de l'énergie mécanique du système : ½kX20 min = ½m v2 min =mgLsin ß X20 min =2mgLsin ß / k ; X0 min =(2mgLsin ß / k )½. X0 min =(2*0,15*9,8*0,80* sin 20 / 35,57 )½=0,15 m = 15 cm.

retour -menu