Dipôle (RLC), laser, concours manipulateur radio Nantes 2009.

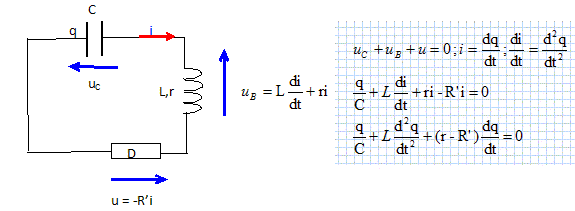
Quelques transferts d'électrons. Une bobine réelle (L,r), un condensateur initialement chargé, un dipôle représentant un montage à « résistance négative» et un interrupteur sont placés en série. La tension aux bomes du montage à « résistance négative» est: u(t) = -R'.i(t). La bobine a une inductance de valeur L = 40,0 mH et une résistance r = 28,2 ohms. Le condensateur est initialement chargé sous une tension uc(t=0) = 4,0 V. A l'instant de date t = 0 s, on ferme l'interrupteur K. Faire un schéma du montage en plaçant le sens arbitraire choisi pour Ie courant électrique et les flèches tensions en convention récepteur pour tous les dipôles. On notera : uc(t) la tension aux bomes du condensateur ; uB(t) la tension aux bomes de la bobine réelle ; u(t) la tension aux bomes du dipôle représentant Ie montage à "résistance négative". Etablir l'équation différentielle (E1) de charge q(t) en fonction des paramètres L, C, r et R'. additivité des tensions aux bornes des dipôles en série. Lq" + (r -R' )q' + q/C = 0 ; q" + (r -R' )/ L q' + q / (LC) = 0 E1. Afin d'obtenir des oscillations sinusoïdales, quelle doit être la valeur de R' ? R' = r. Comment s'écrit l'équation différentielle (E2) dans ce cas ? q" + q / (LC) = 0 E2. D'un point de vue énergétique, quel est le rôle du montage à résistance négative ? 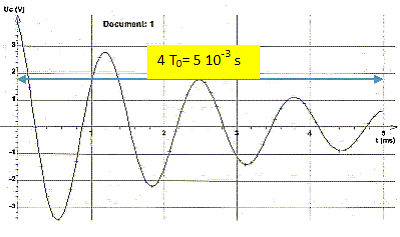A chaque instant, le montage à résistance négative compense les pertes d'énegie par effet Joule dans la résistance de la bobine. La solution de l'équation différentielle E2 est du type : q(t) = qM cos ( 2pi t / T0 + F0) Que représentent les termes qM, T0 et F0 ? qM : charge initiale du condensateur ; T0 : période propre de l'oscillateur LC, F0 : phase à la date t=0. Démontrer l'expression de T0. E2 est de la forme q" + w2 q = 0 avec w2 = 1/(LC) ( oscillateur harmonique) De plus w = 2 pi /T0 d'où T0 = 2 pi ( LC)½. Faire une analyse dimensionnelle de T0. pi est sans dimension ; Emagn = ½ Li2 soit L = 2 Emagn / i2 ; L est une énergie divisée par une intensité au carré. L : J A-2. Eélec = ½ q2 /C soit C = ½ q2 /Eélec; C est une une charge au carré divisée par une énergie de plus une charge est une intensité fois un temps d'où : C : J-1 A2s2 Par suite (LC)½ a la dimension d'un temps. Les enregistrements suivants correspondent au montage sans résistance négative. A partir de la courbe uc(t) déterminer la capacité du condensateur. T0 = 1,25 10-3 s ; C = T02 / (4pi2 L) =[ 1,25 10-3 ]2 /(4*3,142*0,04) =9,9 10-7 F. Identifier les grandeurs énergétiques associées aux courbes. Justifier ? 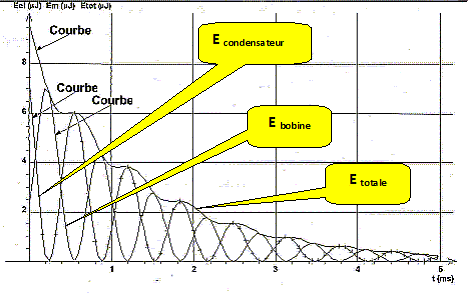A t = 0, le condensateur stocke toute l'énergie du dipôle. La bobine ne stocke pas d'énergie à t = 0. EC + E B = E totale. 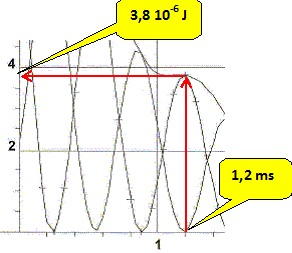Déterminer l'intensité du courant à la date t1 = 1,2 ms. i =(2 EB/ L)½ =(2*3,8 10-6 / 0,04 )½ = 1,378 10-2 A ~ 1,4 10-2 A. Un laser à diode utilisé en chirurgie émet un rayonnement monochromatique, de longueur d'onde dans Ie vide l0 = 810 nm. La puissance du faisceau émis est P = 10 W et la durée de tir est réglable de 10 ms à 100s. c=3,00.108 m.s-l ; h=6,63.10-34 J s; 1 eV= 1,6.10-19 J Quelle est la fréquence f de la radiation lumineuse émise par Ie laser ? fréquence f = c / l0 =3,00.108 / (810 10-9) =3,70 1014 Hz. A quel domaine des ondes electromagnetiques appartient-elle ? Les longueurs d'onde du domaine visible sont comprises entre 400 nm et 800 nm ; 810 nm appartient au proche infrarouge. Quelle est l'energie d'un photon de cette radiation ? Exprimer Ie resultat en Joule, puis en eV. E = h c / l0 =6,63.10-34 *3,00.108 / (810 10-9) =2,46 10-19 J. 2,46 10-19 / 1,6.10-19 =1,5 eV. On dispose de deux échantillons qui contiennent initialement (t = 0) Ie même nombre de noyaux N0. Le premier est forme d'iode 131 de demie vie radioactive t½= 8,0 jours, l'autre est forme de césium 137 de demi-vie t½ = 30 ans. Définir la demi-vie radioactive, la constante de décroissance radioactive l et établir une relation entre ces 2 grandeurs. Demi-vie : durée au bout de l'activité initiale est divisée par deux. Constante radioactive l : le nombre de désintégrations dN se produisant pendant un petit intervalle de temps dtest proportionnel au nombre de radionucléides N présents et à la durée dt : dN = - l Ndt où l est la constante de proportionnalité. Loi de décroissance radioactive : N(t) = N0 exp(-lt) ; N(t½) = ½N0 =N0 exp(-lt½) ; -lt½ = ln(0,5) = - ln 2 ; lt½ = = ln 2. Exprimer, en fonction de N0, Ie nombre N de noyaux présents dans chaque échantillon aux dates t indiquées dans Ie tableau ci-dessous. (L'usage de la loi de décroissance n' est pas nécessaire) date (t) 0 8 jours 1 an 30 ans 300 ans N( iode 131) N0 0,5N0 ~ 0 ~ 0 ~ 0 N( césium 137) N0 ~N0 ~N0 0,5N0 ~ 0 Au bout d'une durée supérieure à 10 t½, l'activité est pratiquement nulle. (1 an est supérieur à 10* 8 jours ; 300 ans est égal à 10 * 30 ans). Pour une durée inférieure à 0,05 t½, l'activité a peu diminué. Lors d'incidents radioactifs, de l'iode 131 et du césium 137 peuvent etre rejetés dans l'atmosphère. Lequel de ces 2 éléments vous semble Ie plus dangereux ? Justifier. La radioactivité due au césium 137 imprégant les sols est importante pendant près de 300 ans alors que la radioactivité due à l'iode 131 disparaît au bout d'un an. Le césium 137 est le plus dangereux. A un instant donné, quel doit être le rapport des deux populations radioactives pour que les deux échantillons aient la même activité ? Exprimer ce rapport en fonction des demies vies. Le calculer. A, l, t½ concerne l'iode 131 et A',l' , t'½ le césium 137. A(t) =l N(t) ; A'(t) =l' N' (t) ; l N = l' N' : N/N' = l' / l. l' = ln 2 / t'½ ; l = ln 2 / t½ ; l' / l = t½ / t'½ ; N/N' = t½ / t'½ = 8 / (30*365) = 7,3 10-4.

c

retour -menu