|
radioactivité, concours paramédicaux : du bismuth au plomb |
|||||||
|
|||||||
|
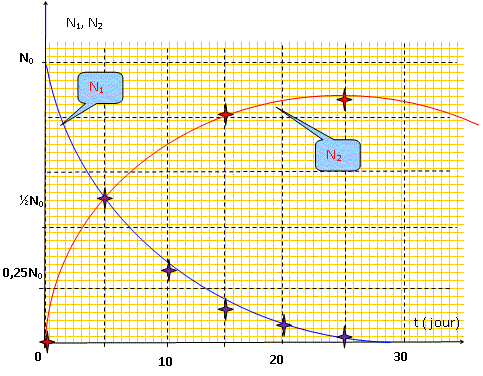
Ecrire les deux équations de désintégration du bismuth en plomb. 21083Bi ---> 21084Po + 0-1e 21084Po ---> 20682Pb +42He
Soient N1(t), N2(t) et N3(t) les nombres respectifs de noyaux de bismuth, de polonium et de plomb. Etablir l'équation différentielle vérifiée par N2(t). Pendant la durée très courte notée dt, dN1 = -l1N1 dt noyaux de bismuth disparaissent par désintégration de type ß- et il apparaît +l1N1 dt noyaux de polonium. Pendant la même durée dt, -l2N2 dt noyaux de polonium disparaissent par désintégration de type alpha. Par suite dN2= l1N1 dt -l2N2 dt dN2/dt + l2N2 =l1N1. Or dN1 = -l1N1 dt donne par intégration : N1 = N0 exp(-l1t) avec N0 nombre de noyaux initiaux de bismuth. D'où : dN2/dt + l2N2 =l1N0 exp(-l1t) (1)
N2= A
exp(-l2t)
avec A une constante. Solution
particulière de
(1)
: N2part = B exp (-l1t)
avec B une constante. dN2part /dt =
-Bl1exp
(-l1t)
puis repport dans
(1) B( l2-l1) =l1N0 ; B = l1N0/( l2-l1) Solution générale de (1) : N2= A exp(-l2t) + l1N0/( l2-l1)exp (-l1t) A t = 0, N2(0) = 0 = A +l1N0/( l2-l1) soit A = - l1N0/( l2-l1) N2= l1N0/( l2-l1) [ exp (-l1t) - exp(-l2t)]. En déduire que N2(t) passe par un maximum et calculer la valeur de t correspondante. Données : le bismuth a une période de 5 jours et le polonium une période de 138,3 jours. dN2/dt = l1N0/( l2-l1) [-l1exp (-l1t) + l2exp (-l2t) ] La dérivée s'annule pour : l1exp (-l1t) = l2exp (-l2t) ; l1 / l2 =exp (-l2t) / exp (-l1t) = exp[(l1 -l2 )t] (l1 -l2 )t = ln (l1 / l2) ; t = ln (l1 / l2) / (l1 -l2 ). On note t½ Bi la demi vie du bismuth : t½ Bi l1 = ln 2 ; l1 = ln 2 / t½ Bi = 0,1386 jour-1. On note t½ Po la demi vie dupolonium : t½ Po l2 = ln 2 ; l2 = ln 2 / t½ Po = 5,01 10-3 jour-1. (l1 / l2) = t½ Po / t½ Bi = 138,3/5 =27,66 ; (l1 -l2 ) =0,1336 jour-1. t = ln 27,66 / 0,1336 = 24,85 jours ~ 25 jours.
|
|||||||
|
|