|
Energie d'un pendule simple : concours orthoptie ( Nantes 2008) |
|||||||
|
|||||||
|
Les vecteurs sont écrits en gras et en bleu. Tracer les forces s'exerçant sur la masse m.
Rappeler le vecteur
accélération pour un mouvement
circulaire uniforme. Justifier la
différence. Dans un mouvement uniforme, la norme du vecteur
vitesse est constante ; en conséquence dv/dt
=0 et a =0
t +
v2/L
n =
v2/L
n. v = L dq/dt ; dériver par rapport au temps : dv/dt = L d2q/dt2. Ecrire les deux équations obtenues par projection de la relation fondamentale de la dynamique. mg + T = ma s'écrit en projection sur : n : T - mg cos q =mv2/L. t : 0 - mg sin q = m dv/dt. Montrer que q satisfait à une équation de la forme d2q/dt2 + w2 sin q =0. En déduire la période des petites oscillations du pendule. - mg sin q = m dv/dt = m L d2q/dt2 ; L d2q/dt2 +g sin q =0 On pose w2 = g/L d'où d2q/dt2 + w2 sin q =0. Pour les angles petits on peut confondre sin q avec q radian. d2q/dt2 + w2 q =0, équation différentielle d'un oscillateur harmonique de période T = 2p/w = 2p(L/g)½. Déterminer T en fonction de m, g, v, L et q. T - mg cos q =mv2/L ; T = m[ v2/L + g cos q ].
A la position initiale, la vitesse est nulle, l'énergie mécanique est sous forme potentielle de pesanteur. On choisit l'origine des altitudes à la position d'équilibre.
En déduire l'énergie cinétique de m pour un angle q quelconque en fonction de m, g, L, q0 et q. Energie mécanique pour un angle q quelconque : EM= mg L (1-cos q ) + Ec. En absence de frottement, l'énergie mécanique se conserve : mg L (1-cos q ) + Ec = mg L (1-cos q0 ) Ec =mg L (cos q - cos q0 ). Montrer que T s'écrit : T = mg(3 cosq - 2 cosq0). Ec =mg L (cos q - cos q0 ) = ½mv2 ; v2 / L = 2g (cos q - cos q0 ). Or T= m[ v2/L + g cos q ] d'où T = 2mg (cos q - cos q0 ) + mg cos q . T = mg(3 cosq - 2 cosq0).
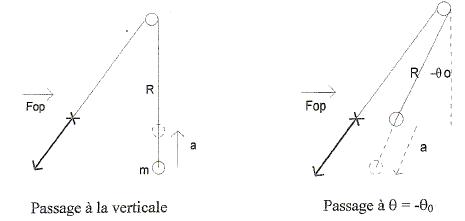
Lors de la première oscillation on pourra utiliser l'expression de la tension trouvée ci-dessus. Au premier passage à la verticale, la longueur du pendule est réduite de a ( a faible devant L)
|
|||||||
|
|
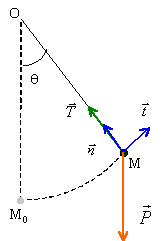 Poids
et tension du fil T.
Poids
et tension du fil T.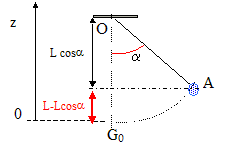 EM=
mg L (1-cos q0
).
EM=
mg L (1-cos q0
).