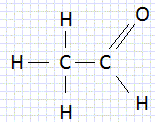Ester, oxydoréduction : constante d'équilibre, quotient de réaction concours kiné Nantes 2009.

Un ester E a une formule brute C6H12O2. L'hydrolyse en milieu acide (H2SO4) de cet ester donne deux composés A et B. Le composé B peut être obtenu par oxydation ménagée de A. Identifier A, B et E. Nommer les. L'hydrolyse donne un acide carboxylique et un alcool. L'oxydation ménagée conserve le squelette carboné : A et B possèdent le même nombre d'atomes de carbone soit 6 / 2 =3. B : CH3-CH2-COOH acide propanoïque. Seul un alcool primaire conduit par oxydation ménagée à un acide carboxylique. A : CH3-CH2-CH2OH propan-1-ol. E : CH3-CH2-COO-CH2-CH2-CH3 propanoate de propyle. Ecrire l'équation chimique de l'hydrolyse de E. CH3-CH2-COO-CH2-CH2-CH3 + H2O = CH3-CH2-COOH + CH3-CH2-CH2OH.  Préciser ces caractéristiques. Quel est le rôle de l'acide sulfurique ? Comment s'appelle la réaction inverse ? L'hydrolyse de l'ester est lente, athermique et limitée. L'acide sulfurique joue le rôle de catalyseur. La réaction inverse de l'hydrolyse est l'estérification. Un mélange initial, constitué d'une mole d'ester et d'une mole d'eau, conduit à un mélange final ne contenant plus que 0,66 mol d'ester. Déterminer la constante d'équilibre K de la réaction d'hydrolyse. avancement (mol) E +H2O = A +B initial 0 1 1 0 0 intermédiaire x 1-x 1-x x x fin xf = 0,34 1-xf =0,66 1-xf =0,66 xf = 0,34 xf = 0,34 On note V(litre) le volume de la solution [E]f = [H2O]f=0,66/V ; [A]f =[B]f =0,34 / V K= [A]f[B]f / ([E]f[H2O]f) = (0,34/0,66)2 =0,2654 ~ 0,27. Un mélange initial, constitué d'une mole d'ester et de n moles d'eau, conduit à un mélange final ne contenant plus que 0,30 mol d'ester. Déterminer n. avancement (mol) E +H2O = A +B initial 0 1 n 0 0 intermédiaire x 1-x n-x x x fin xf = 0,70 1-xf =0,30 n-xf =n-0,70 xf = 0,70 xf = 0,70 On note V(litre) le volume de la solution [E]f 0,30 / V ; [H2O]f=(n-0,70)/V ; [A]f =[B]f =0,70 / V. 0,2654 = 0,702 / (0,30(n-0,70)) ; 0,0796 (n-0,70) = 0,49 ; n = 0,70 +6,15 ; n = 6,9. On fait réagir l'ester avec une solution concentrée d'hydroxyde de sodium. Ecrire l'équation chimique de la réaction. Préciser le nom et les caractéristiques de cette réaction. CH3-CH2-COO-CH2-CH2-CH3 + (Na+ + HO-) = CH3-CH2-COO- +Na+ + CH3-CH2-CH2OH.  La saponification ( hydrolyse basique ) de l'ester est lente et totale. Réaction d'oxydoréduction. La constante d'équilibre de la réaction suivante est K = 3,2. Ag+aq + Fe2+aq = Ag(s) + Fe3+aq. On introduit dans un becher V1 = 100 mL d'une solution aqueuse d'ion Ag+aq de concentration c1 = 0,10 mol/L et V2 =100 mL d'une solution aqueuse d'ion Fe2+aq de concentration c2 = 0,20 mol/L. Quelle est la valeur initiale Q r i du quotient de réaction ? Dans quel sens évolue le système ? Q r i = [Fe3+aq]i / ([Ag+aq]i [Fe2+aq]i) ; or [Fe3+aq]i = 0 donc Q r i =0. Q r i < K, donc évolution spontanée dans le sens direct.  Calculer les concentrations des différents ions lorsque l'équilibre est atteint. avancement (mol) Ag+aq + Fe2+aq = Ag(s) + Fe3+aq initial 0 c1V1 =0,01 c2V2 =0,02 0 0 intermédiaire x 0,01-x 0,02-x x x fin xf 0,01-xf 0,02-xf xf xf [Ag+aq]f =(0,01-xf) / (V1 +V2 ) = (0,01-xf) /0,2 = 5 (0,01-xf) [Fe2+aq]f =(0,02-xf) / (V1 +V2 ) = (0,02-xf) /0,2 = 5 (0,02-xf) [Fe3+aq]f =xf / (V1 +V2 ) = xf /0,2 = 5 xf. K = [Fe3+aq]f / ([Fe2+aq]f [Ag+aq]f ) ; 3,2 = xf / [5(0,01-xf)(0,02-xf)] 16(0,01-xf)(0,02-xf) = xf ; xf2 -0,0925 xf +2 10-4 =0 ; xf = 2,215 10-3. [Ag+aq]f =5 (0,01-xf)=5(0,01-2,215 10-3) =3,892 10-2 mol/L. [Ag+aq]f ~ 3,9 10-2 mol/L.   [Fe2+aq]f =5 (0,02-xf) = 5 (0,02 -2,215 10-3) =8,893 10-2 mol/L. [Fe2+aq]f ~ 8,9 10-2 mol/L.   [Fe3+aq]f = 5 xf = 5*2,215 10-3 =1,108 10-2 mol/L. [Fe3+aq]f ~ 1,1 10-2 mol/L.   Quelle masse d'argent métal obtient-on à l'équilibre ? m = xf M = 2,215 10-3 *108 =0,239 g ~ 0,24 g. On plonge une tige d'argent dans la solution. Que se produit-il ? Justifier. Le quotient de réaction et la constante d'équilibre sont indépendants de la masse d'argent : donc il ne se passe rien. Oxydation et thermolyse de l'éthanal. L'éthanal est un aldehyde de formule brute C2H4O. Donner sa formule développée. On réalise l'oxydation ménagée de l'éthanal par action d'une solution aqueuse de permanganate de potassium en milieu acide. Ecrire l'équation chimique de la réaction d'oxydoréduction. couple MnO4- / Mn2+ : 2 fois { MnO4- +8H+ + 5e- = Mn2+ +4H2O} couple C2H4O2 / C2H4O : 5 fois { C2H4O + H2O = C2H4O2 + 2H+ + 2e- } 2MnO4- +6H+ + 5 C2H4O = 2 Mn2+ +5 C2H4O2 + 3 H2O. A température élevée, l'éthanal se décompose en phase gazeuse selon : C2H4O(g) --> CH4 (g) + CO(g) Cette thermolyse esr réalisée dans un récipient clos de volume constant à la température constante de 480 °C. on étudie la cinétique de la réaction en mesurant la pression totale P du mélange gazeux au cours du temps. t(min) 0 20 40 60 80 100 P(bar) 0,42 0,54 0,61 0,65 0,68 0,70 La réaction de thermolyse étant totale, quelle sera la pression Pf en fin de réaction ? Justifier. avancement (mol) C2H4O(g) --> CH4 (g) + CO(g) initial 0 n0 0 0 intermédiaire x n0 -x x x fin xf = n0 n0 -xf = 0 xf = n0 xf = n0 Nombre total de moles à la fin de la thermolyse : n0 +xf = 2 n0. La température et le volume sont constants ; la quantité de matiète finale des gaz est égale à 2 fois la quantité de matière initiale du gaz. Or P = n RT/V = constante * n. La pression finale sera donc égale à deux fois la pression initiale : Pf = 2*0,42 = 0,84 bar. Tracer la courbe P= f(t). 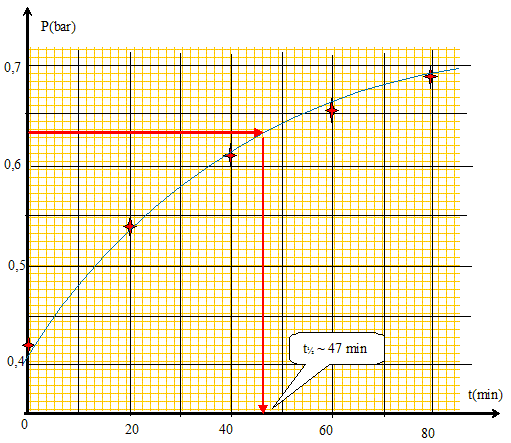Définir le temps de demi-réaction t½. Durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. Calculer la pression totale P=P½ à la date t½. Déterminer graphiquement t½. xf = n0 ; xt½ = 0,5 n0 ; ntotal =n0 + 0,5 n0 = 1,5 n0 ; or pression et quantité de matière sont proportionnelles, d'où : P½ = 1,5 Pinitiale P½ =1,5*0,42 =0,63 bar.

c

retour -menu