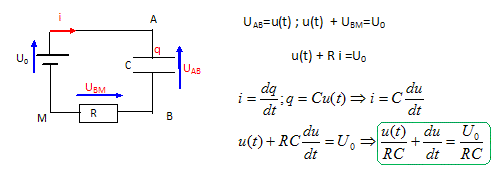QCM électromagnétisme, physique nucléaire ( Kiné St Michel 2009)

Condensateur. Soit un condensateur de capacité C aux bornes duquel on applique une tension électrique U. Les plaques du condensateur sont distantes d'une distance d. On rapproche les plaques à une distance ½d. Analyse : A- la capacité du nouveau condensateur est multipliée par 2. Vrai. La capacité C est égale à : C = e S/d avec S : surface d'une plaque et d : distance des plaques. B- la charge du nouveau condensateur est multipliée par 2. Vrai. Charge q = C U avec U constante liée au générateur. C- La tension du nouveau condensateur est divisée par 2. Faux. Le générateur impose la tension U aux bornes du condensateur. D- L'énergie du nouveau copndensateur est multipliée par 4. Faux. E = ½CU2 ; U est constant, C double : l'énergie double. E- L'énergie du nouveau copndensateur est la même que celle du premier. Faux. Dipôle (RC). On charge un condensateur sous une tension U0=10 V à travers un conducteur ohmique de résistance R = 10 kW. A l'instant t=0 la charge du condensateur est nulle et au bout d'un temps très long, la charge du condensateur vaut Q= 500µC. On note u(t) la tension aux bornes du condensateur. Analyse : A- On peut écrire u(t) / (RC) + du(t) / dt = U0. Faux. à gaucheles 2 termes sont homogènes à : V T-1 ; à droite le terme est homogène à une tension. B- la capacité vaut C = 50 µF. Vrai. Charge maximale Q = CU0 = 500 µC ; C = 500 / U0 = 500/10 = 50 µF. C-La constante de temps vaut t = 0,50 ms. Faux. t =RC = 10 103 * 50 10-6 =0,5 s = 500 ms. D- Après une durée égale à t la charge vaut 90 % de sa valeur maximale. Faux. à t = t , la charge vaut 63 % de sa valeur maximale. 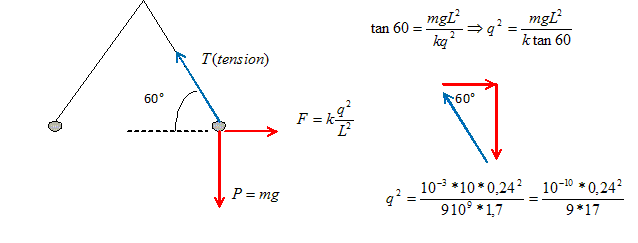Pendule électrique. On considère dans le vide de permitivité e0 deux charges électriques ponctuelles identiques de charge q et de masse m. Elles sont suspendues à un point fixe O par deux fils sans masse, inextensibles et isolants de même longueur L. La valeur de la charge q pour que la figure soit un triangle équilatéral est : A B C( vrai) D E 4,0 10-7 C 2,4 10-7 C 2,0 10-7 C 3,20 10-7 C 5,0 10-7 C L=0,24 m ; m = 1,0 g ; g = 10 m s-2 ; 6½ =2,5 ; 10½ =3 ; 17½ ~4. tan 45 = 1 ; tan 30 =0,6 ; tan 60 = 1,7 ; k=9 109 SI. Analyse : q = 0,24 10-5 / (3*4) = 2,0 10-7 C. 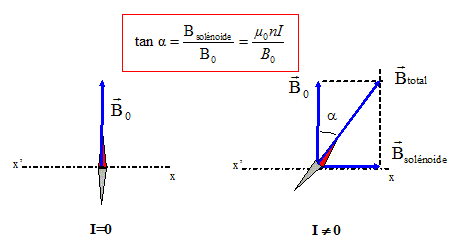Solénoïde Un solénoïde très long est constitué par une couche de fil isolé à spires jointives. Le fil a un diamètre d = 2,0 mm. L'axe du solénoïde est perpendiculaire au méridien magnétique. On place dans la réfgion centrale une boussole. Lorsqu'on établit le courant, l'aiguille tourne de 30 °. La composante horizontale du champ magnétique terrestre ayant pour valeur 2,0 10-5 T, l'intensité du courant est :   A B C( vrai) D E 17 mA 5 mA 20 mA 10 mA 30 mA cos 30 = 0,9 ; sin 30 = 0,5 ; tan 30 = 0,6 et µ0 =1,2 10-6. Analyse : nombre de spires par mètre : n = 1/ 2,0 10-3 =500. I = B0 tan 30 / (µ0 n)=2,0 10-5 *0,6 /(1,2 10-6 *500)=1,2 / (1,2 *50) = 1/50 = 0,02 A = 20 mA. Inductance. Un enroulement d'électroaimant a une inductance de 50 H ; il est parcouru par un courant de 20 A. Sur quelle hauteur pourrait-on soulever une masse de 1 kg avec une énergie de même valeur que celle emmagasinée dans la bobine ? A( vrai) B C( vrai) D E 1000 m 50 m 1 km 500 m 200 m Analyse : Energie stockée dans la bobine : E = ½LI2 = 0,5*50*202 =25*400 =1,0 104 J. Variation d'énergie potentielle de la masse de 1 kg : mgh = 1,0*10*h = 10 h d'où h = 1,0 104/10 =1000 m = 1 km.   radioactivité ß-. Pour que l'émission d'une source émettrice ß- soit équivalente à un courant électrique d'intensité 10 mA, l'activité de la source est : A( vrai) B C D E 6,25 1016 Bq 1,6 1016 Bq 12,5 1016 Bq 3,08 1016 Bq 3,08 1015 Bq Analyse : I = n e ; e : charge élélentaire 1,6 10-19 C et n nombre d'électrons traversant une section droite du conducteur à chaque seconde. Activité : nombre de désintégrations par seconde = nombre d'électrons émis par seconde. n = 0,01 / 1,6 10-19 =1017/1,6 ~6,25 1016. Activité. Un barreau de combustible irradié extrait a une activité A1 = 3,7 1013 Bq. 50 % de son activité est due au rayonnement gamma. La demi épaisseur de plomb pour l'absorption gamma est égale à 1 cm. Pour que l'activité mesurée à l'extérieur soit divisée par 106 l'épaisseur de plomb entourant le barreau doit être égale à : A B C ( vrai) D E 10 cm 5 cm 20 cm 40 cm 50 cm ln2 =0,7 et ln 10-6 = -14 Analyse : A = A1 exp(-µ x) ; ln ( A1/A) = µ x, avec µ une constante et x l'paisseur de plomb. si A1/A = 2 et x= 1 cm : µ = ln 2 cm-1. si A1/A = 106 : x = ln 106 / µ = 14 / ln2 = 14 / 0,7 = 20 cm. loi de décroissance radioactive Un échantillon de noyaux radioactifs a une constante radioactive l égale à ½ln2 dans le système SI. Au bout de 1 s : Analyse : l t½ = ln 2 ; t½ = ln2/ l = ln2 / ln2 * 2 = 2 s. A- aucune désintégrations n'a encore eu lieu. Faux. Au bout de deux secondes la moitié des noyaux initiaux se sont désintégrés. B- 30% des noyaux père se sont désintégrés. Vrai. N= N0 exp(-lt) ; ln (N0/N) = lt avec t = 1 s ; ln (N0/N) = ln2/2 = ln2½ ; N0/N = 2½ ~1,4 ; N = N0/1,4 ~ 0,7 N0. C-il reste 25 % du nombre initial de noyaux père. Faux. D- il reste 70 % du nombre initial de noyaux père. Vrai. énergie de liaison A-L'énergie de liaison est l'énergie fournie lors de la formation du noyau à partir de ses nucléons isolés et immobiles. Faux. On appelle énergie de liaison notée El d'un noyau l'énergie que doit fournir le milieu extérieur pour séparer ce noyau au repos en ses nucléons libres au repos. B- L'énergie de liaison par nucléon est plus grande pour les noyaux légers que pour les noyaux lourds. Faux. Elle est faible pour les noyaux légers, augmente jusqu'au fer 56 et décroît ensuite. C-Plus un noyau est stable, plus son énergie de liaison est élevée. Faux. Un noyau est d'autant plus stable que son énergie de liaison moyenne par nucléon est grande. D-L'énergie de liaison des nucléons stables est de l'ordre de 8 MeV/nucléon.Faux. Il faudrait écrire " L'énergie de liaison par nucléon des nucléides stables..." E- l'énergie de liaison est définie par : El = défaut de masse *c2. Vrai. On appelle défaut de masse d'un noyau la différence entre la masse totale des A nucléons séparés ( Z protons et A-Z neutrons), au repos et la masse du noyau formé, au repos El = D mc².

retour -menu