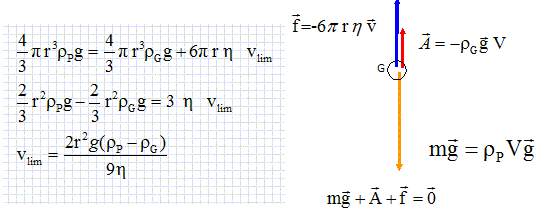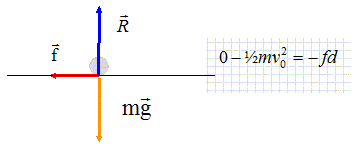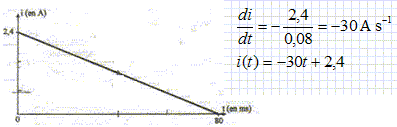QCM mécanique, électricité, optique ( concours ergothérapie Berck 2009)

Une bille sphérique en porcelaine et de rayon r est lâchée sans vitesse initiale dans une éprouvette contenant de la glycérine. Au cours de sa chute la bille est soumise aux forces suivantes : On écrit les vecteurs en gras et en bleu. - son poids P ; - la poussée d'Archimède A ; - la force de frottement fluide f = -k v avec k = 6 p h r ; h : viscosité ( Pa s) de la glycérine. Masse volumique de la glycérine rG =1,3 g/mL ; masse volumique de la porcelaine rP =2,3 g/mL ;rayon de la bille r = 1,0 cm ; h = 1,0 Pa s ; g = 10 N/kg ; volume d'une sphère V = 4/3 pi r3. calculer la valeur de la vitesse limite ( en m/s). A B ( vrai) C D E F 0,11 0,22 0,33 0,44 0,55 aucune réponse exacte Analyse : La vitesse limite étant atteinte,le mouvement est rectiligne uniforme ; les forces se compensent :   vlim =2*10-4 *10(2300-1300)/9 =2/9 = 0,22 m/s. Un palet de masse m=100 g est lancé sur une surface horizontale recouverte de glace avec une vitesse initiale v0 = 10 m/s. Le palet s'arrête après avoir parcouru d = 50 m. On modèlise les frottements par une force constante, directement opposée au vecteur vitesse. Calculer la vitesse initiale du palet s'il s'arrête au bout de 32 m ( en m/s). A B C D E( vrai) F 4,0 5,0 6,0 7,0 8,0 autre Analyse : Ecrire le théorème de l'énergie cinétique : Premier lancer : f = 0,5 *0,1 *102 / 50 =5/50 = 0,1 N. Second lancer : v02 = 2fd/m = 2*0,1*32/0,1 =64 ; v0 = 8,0 m/s. Un oscillateur est constitué par un solide de masse m =200 g accroché à l'extrémité libre d'un ressort à spires non jointives, de masse négligeable, de constante de raideur k. le solide oscille sans frottement suivant un plan horizontal. la période propre de cet oscillateur est T0 = 0,80 s. L'amplitude est a =2,0 cm. pi2 ~ 10. Déterminer l'énergie mécanique ( mJ) de cet oscillateur. A B C( vrai) D E F 1,0 1,8 2,5 3,4 4,2 autre Analyse : T0 = 2 pi [m / k]½ ; k = 4 pi2 m / T20 =4*10*0,2/0,82 =8/0,64 = 1/0,8 = 12,5 N/m. Lorsque le centre d'inertie de la masse pase par la position a = 2,0 cm, l'énergie mécanique est sous forme d'énergie potentielle élastique : E =½ka2. E = 0,5*12,5 * 4 10-4 = 2,5 10-3 J = 2,5 mJ. Une balle est lâchée sans vitesse initiale d'une hauteur de 10 m au dessus du sol. On néglige l'action de l'air sur la balle. On suppose que la balle effectue une série de rebonds verticaux et que l'énergie cinétique juste après un rebond diminue de 10% par rapport à l'énergie cinétique juste avant. Déterminer la hauteur maximale ( en m) à laquelle la balle remontera après le second rebond. A B C D E( vrai) F 1,2 2,4 4,8 7,2 8,1 autre Analyse : Juste avant le premier rebond, l'énergie cinétique est : mgh = ½mv2. Juste après le premier rebond, l'énergie cinétique vaut : 0,9 mgh. Juste avant le second rebond, l'énergie cinétique est : 0,9 mgh. Juste après le second rebond, l'énergie cinétique vaut : 0,9*0,9 mgh = 0,81 mgh. La bille remonte d'une hauteur h' telle que : mgh' = 0,81 mgh ; h' = 0,81 h = 0,81*10 = 8,1 m. Une bobine d'inductance L = 80 mH et de résistance r = 5,0 ohms est parcourue par un courant dont l'intensité varie comme l'indique le graphe: Calculer en volt la tension aux bornes de la bobine à la date t = 60 ms. A ( vrai) B C D E F 0,60 0,80 1,0 1,2 1,4 autre Analyse : u =Ldi/dt + r i = 0,08 (-30) +5(-30t +2,4) = -2,4 -150t +12 = 9,6 -150 t. u( t = 0,06) = 9,6-150*0,06 = 0,6 V. 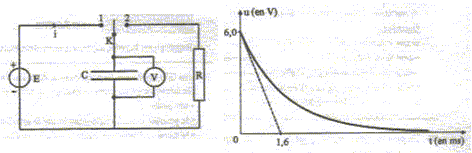R = 100 ohms ; e = 6,0 V. 1ère étape : l'interrupteur K est en position 1 pendant le temps nécessaire pour que le condensateur se charge complètement. 2ème étape : l'interrupteur K bascule en position 2. La courbe indique l'évolution de la tension aux bornes du condensateur en fonction du temps. On a représenté la tangente à l'origine. Calculer en µF la capacité C du condensateur. A B C ( vrai) D E F 0,16 1,6 16 32 64 autre Analyse : Constante de temps RC = 1,6 10-3 s ( lecture graphe : intersection de la tangente avec l'axe des temps) C = 1,6 10-3 / R = 1,6 10-3 /100 = 1,6 10-5 F = 16 10-6 F = 16 µF.   Un objet réel AB est placé à 40 cm devant une lentille mince convergente de centre optique O, de distance focale f'. AB assimilable à un segment est perpendiculaire à l'axe optique et le point A est sur l'axe. On déplace un écran jusqu'à observer l'image de AB donnée par la lentille. On constate que l'image a la même dimension que l'objet. Combien y a t-il d'affirmations exactes ? A ( vrai) B C D E F 1 2 3 4 5 autre Analyse :  vergence = 1/f' = 1/0,2 = 5 dioptries. - la vergence de la lentille est 0,05 dioptrie ( faux) - l'image a le même sens que l'objet ( faux) - tous les rayons qu sortent de la lentille passent par le foyer principal image (faux) - l'image est réelle ( vrai ) - l'écran se situe à 80 cm de l'objet ( faux ). 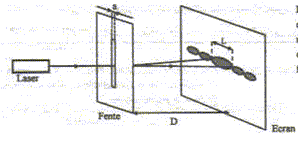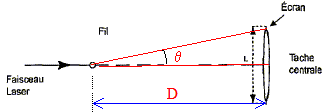Longueur d'onde l = 0,6328 µm ; D = 2,00 m ; a = 0,20 mm calculer la largeur de la tache centrale de diffraction ( en cm). A ( vrai) B C D E F 1,3 2,6 3,2 4,6 5,2 autre Analyse : tan q = ½L/D voisin de q radian pour les angles petits. d'autre part q = l/a. avec : l longueur d'onde (m) et a : diamètre du fil (m) en tenant compte des deux relations ci-dessus : ½L/D=l/a soit a=2lD/L ou L = 2l D/a. L= 2* 0,6328 10-6*2,00/ 2,0 10-4 = 0,6328 10-2*2,00= 1,26 10-2 m ; L = 1,3 cm.

retour -menu