Optique, mouvement d'un skieur : concours ergothérapie Créteil et Adere 2009.

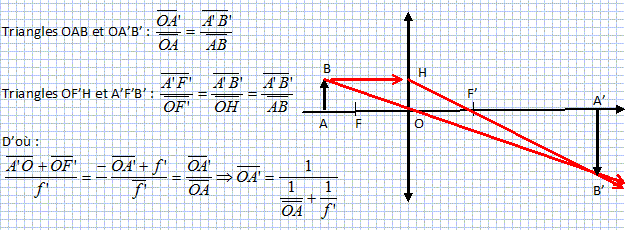
Créteil. Soit une lentille convergente de vergence C=5 dioptries. calculer la distance focale f' de cette lentille. f' = 1/C = 1/5 = 0,2 m = 20 cm. Soit un objet AB ( A sur l'axe optique) placé perpendiculairement à l'axe optique et A'B' son image par la lentille convergente. On écrit les distances algébriques en gras et en bleu. Etablir l'expression littérale de OA' en fonction de OA et f'. Cet objet se trouve à une distance de 15 cm en avant du centre optique de la lentille. Caractériser l'image obtenue. Quel est l'effet obtenu ? 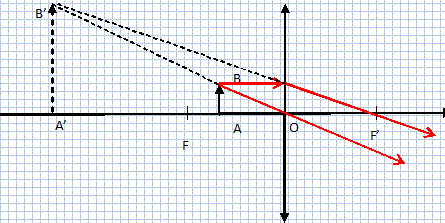1/OA = 1/(-0,15) = -100/15 = - 20/3 ; 1/f' = 5 ; 1/OA +1/f' =-20/3 +15/3 = -5/3 ; OA' = -3/5 = - 0,6 m. (image virtuelle) Grandissement transversal : OA' /OA =-0,6 / (-0,15) = 4. Image droite ( même sens que l'objet) ; image 4 fois plus grande que l'objet. 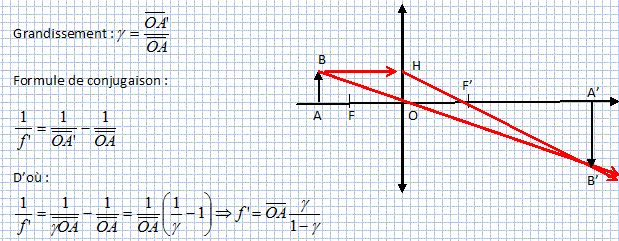La lentille fonctionne en loupe. On retire la première lentille et on la remplace par une lentille de vergence inconnue. Pour cette lentille convergente on obtient un grandissement g = -2 pour un objet placé à une distance de 1,2 m en avant de la lentille. Etablir l'expression littérale de la distance focale f' en fonction de g et de OA. Calculer f'. f' = -1,2*(-2)/3 = 2,4/3 = 0,8 m. Calculer AA' et en déduire la distance entre l'objet et l'image. AA' = AO +OA' =-OA +gOA =OA(g-1) = -1,2(-3) = 3,6 m. Distance objet-image : 3,6 m. Adere. 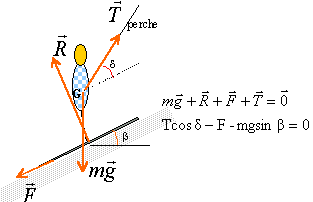Un skieur de masse M =90 kg portant un équipement de masse méq,tiré par une perche d'un remonte pente, gravit à vitesse constante une pente enneigée faisant un angle de 30° avec le plan horizontal. L'ensemble des forces de frottements a une valeur de 500 N dans toute cette partie. g = 10 N/kg ; sin 30 = 0,5 ; cos 30 = 3½/2 ; 10½=3,16. Faire le bilan des forces extérieures qui s'exercent sur le système et schématiser la situation. D'après le principe d'inertie la somme des forces est nulle. Projection suivant un axe parallèle au plan vers le haut. Calculer la masse méq sachant que la perche tracte le skieur avec une force d'intensité T = 1000 N. m= M+méq= (T cosd -F) /(gsinb). Hypothèse : T cos d = 1000 N ; méq=(T cosd -F) /(gsinb)-M = (1000-500) / (10*0,5)-90 =500 / 5 -90= 100-90 =10 kg. Après 300 m, le skieur s'arrête et se débarrasse de son équipement. Il gravit ensuite avec le remonte pente avec la même force T, la distance d=100 m qui le sépare du sommet, avec une accélération constante. Déterminer les équations horaires du mouvement sur ce parcours et en déduire la durée qu'il mettra pour arriver au sommet. Le bilan des forces est identique ; la seconde loi de Newton, projeté sur un axe parallèle au plan, orienté vers le haut, s'écrit : T cosd -F -Mg sin ß = Ma ; a = (T cosd -F)/M-g sin ß = (1000-500)/90-10*0,5 = 50/9 -5 = (50-45)/9 = 5/9 m s-2. La vitesse est une primitive de l'accélération et la vitesse initiale est nulle : v(t) = a t. La position est une primitive de la vitesse et la position initiale est l'origine de l'axe : x=½at2 = 5/18t2 . Durée pour arriver au sommet : t = (2d/a)½=(200*9/5)½ = 360½ = 6*10½ = 6*3,16 = 18,96~ 19 s. Une fois au sommet il fait un saut de 80 m sur l'autre versant de la piste, sans vitese initiale. Avec quelle vitesse arrivera t-il au sol en fin de parcours, si on néglige les frottements ? Hypothèse : la différence de hauteur entre le point de départ et le point d'arrivée est h = 80 m. On choisit comme origine des altitudes, celle du point d'arrivée. L'énergie mécanique initiale du skieur est sous forme potentielle de pesanteur : E = mgh. L'énergie mécanique finale du skieur est sous forme cinétique : ½mv2. Seul le poids travaille, l'énergie mécanique reste constante : ½mv2 = mgh v =(2gh)½ = (2*10*80)½ =1600½ = 40 m/s.

c

retour -menu