QCM virage circulaire, solénoïde, fusion nucléaire, dipôle RLC, moteur électrique ( Kiné EFOM 2009)

On peut considérer que les actions qui s'exercent sur un avion en vol sont équivalentes à 4 forces : - le poids P ; - la poussée F due aux réacteurs : - la trainée représentant les frottements et la résistance de l'air à l'avancement ; dans cet exercice cette force est considérée comme négligeable ; - la portance R représentant l'action de l'air sur les ailes de l'avion et résultant des différences de pression entre les parties inférieure et supérieure de l'avion ; elle est toujours dans le plan de symétrie de l'avion, perpendiculaire au plan des ailes. On donne g = 10 m s-2. Un avion de masse 2 tonnes, partant du repos, parcourt la totalité de la plate forme horizontale d'un porte avions, supposé immobile, avant de décoller. La longueur de la piste d'envol est de 200 m et la vitesse au bout de la piste est de 360 km/h. Evaluer l'intensité de la force de propulsion F supposée constante. A B C D E F ( vrai) 15800 N 22300 N 44100 N 30000 N 37000 N autre Analyse : Poids et action du plan sont perpendiculaires à la vitesse : elles ne travaillent pas Travail de la force de propulsion : W = F * d = 200 F variation d'énergie cinétique : ½mv2-0 avec m = 2000 kg et v = 360/3,6 = 100 m/s ½mv2 = 1000*1002 = 10 7 J. théorème de l'énergie cinétique : 10 7 = 200 F ; F = 10 7 / 200 = 50000 N. virage circulaire. Le même avion attaque à la vitesse constante de 720 km/h un virage circulaire horizontal de 800 m de rayon Déterminer la norme du vecteur accélération ( m s-2) de l'avion . 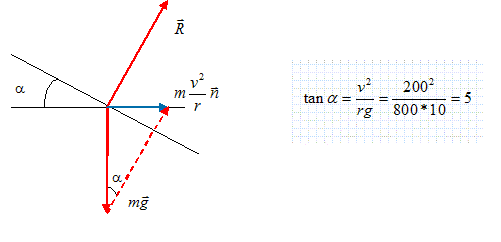A( vrai) B C D E F 50 5,5 12 42 61 autre Analyse : accélération centripète aN = v2/rayon avec v = 720/3,6 = 200 m/s aN = 2002/800 = 50 m s-2. inclinaison des ailes. Déterminer l'inclinaison a des ailes, supposées planes, par rapport au plan horizontal. A B C ( vrai) D E F sin a =0,7 cos a =0,7 tan a =5 sin a =0,5 cos a =0,6 autres Analyse : solénoïde. Un solénoïde est parcouru par un courant d'intensité I = 2 A ; sa longueur est L = 20 cm, son rayon r = 4 cm. Il est formé de 800 spires de fil de cuivre isolé, la résistance de l'ensemble est de 4 ohms. µ0 = 1,25 10-6 SI. Quelle est la valeur du champ magnétique à l'intérieur du solénoïde ? A B C D( vrai) E F 100 mT 240 mT 45 mT 10 mT 0,5 T autre Analyse : Nombre de spires par mètre : n = 800/0,20 = 4000 spires par mètre Champ magnétique B = µ0 n I = 1,25 10-6 *4000 *2 = 1,0 10-2 T = 10 mT. Quelle est la fem E du générateur de résistance interne r = 1 ohm branché aux bornes du solénoïde ? A ( vrai) B C D E F 10 V 6 V 12 V 5,5 V 3 V autre Analyse : tension aux bornes du générateur U = E-r I = E-1*2 = E-2 V tension aux bornes du solénoïde U = R I = 4*2 = 8 V Par suite E-2 = 8 ; E = 10 V fusion nucléaire 21H + 21H = 31H + 11H. L'énergie de liaison par nucléon est 1,11 MeV pour le deutérium et 2,83 MeV pour le tritium. Déterminer l'énergie libérée au cours de cette réaction. A ( vrai) B C D E F 4,05 Mev 2,86 MeV 6,46 MeV 3,18 MeV 5,37 MeV autre Analyse : Le tritium compte 3 nucléons : 3 El(31H) = 3*2,83 = 8,49 meV Le deutérium compte 2 nucléons : 2 El(21H) = 2*1,11 = 2,22 meV Energie libérée : 3 El(31H) -2 El(21H) -2 El(21H) = 8,49-2,22-2,22 =4,05 MeV. dipôle RLC. 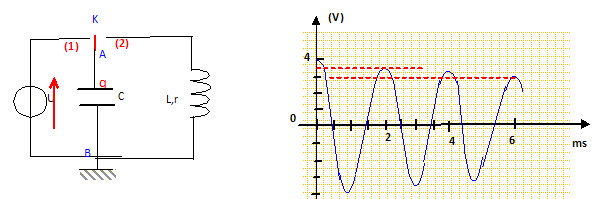Le condensateur de capacité C = 1 µF est préalablement chargé par le générateur de fem E =4 V ( interrupteur en position 1). On enregistre la tension uc(t) aux ornes du condensateur en basculant l'interrupteur en position 2. L'instant du basculement est choisi comme origine des dates. Déterminer l'énergie initialement fournie au dipôle RLC. A B C D E ( vrai) F 8 mJ 3 µJ 320 µJ 165 mJ 8 10-6 J autre Analyse : Energie stockée par le condensateur à t=0 : ½CE2 =0,5* 10-6*42 =8 10-6 J = 8 µJ Cette énergie est fournie au dipôle RLC.   Au bout d'une pseudopériode, déterminer l'énergie totale stockée dans le dipôle RLC. A B C D ( vrai) E F 6,3 mJ 285 µJ 2,7 µJ 6,1 µJ 148 mJ autres Analyse : à t = T, la tension aux bornes du condensateur est 3,5 V. Le condensateur stocke toute l'énergie du dipôle. Energie stockée : ½CU2 = 0,5 10-6 *3,52 = 6,1 10-6 J = 6,1 µJ. Calculer la puissance moyenne perdue en une pseudo-période. A B ( vrai) C D E F 0,85 µW 0,95 mW 2,35 mW 148 µW 5,5 mW autre Analyse Puissance (W) = énergie (J) / durée (s). Le dipôle perd 8-6,1 = 1,9 µJ = 1,9 10-6 J en 2 10-3 s. Pmoyenne = 1,9 10-6 /2 10-3 = 0,95 10-3 W = 0,95 mW. Moteur électrique. Un moteur électrique ( fcem E' = 1,25 V, r' = 1 ohm) est associé en série avec un générateur ( fem E = 4,5 V, r = 1,5 ohms) et un conducteur ohmique R = 4 ohms. Intensité du courant dans le circuit . A( vrai) B C D E F 0,5 A 1 A 0,05 A 0,1 A 1,2 A autres Analyse : additivité des tensions : E-ri = RI + E'+r'I ; I = (E-E') / (R+r+r') I = (4,5-1,25) / (4+1+1,5) =3,25 / 6,5 = 0,5 A. 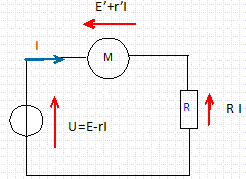Calculer pour 3 min de fonctionnement, l'énergie totale fournie par la pile. A B C D( vrai) E F 125 J 250 J 12,5 J 405 J 35 J autre Analyse : Energie fournie : E I t avec t = 60*3 = 180 s et E=4,5 V. 4,5 * 0,5 *180 = 405 J. Calculer pour 3 min de fonctionnement, l'énergie consommée dans le conducteur ohmique. A B C D E F( vrai) 125 J 250 J 215 J 405 J 35 J autre Analyse : R I2 t = 4*0,52*180 = 180 J Calculer pour 3 min de fonctionnement, l'énergie utile produite par le moteur. 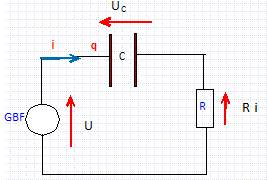A B C D E ( vrai) F 125 J 250 J 12,5 J 405 J 112,5 J autre Analyse : E' I t = 1,25*0,5*180 = 112,5 J. dipôlr RC. C = 20 µF ; R = 500 ohms. le GBf délivre une tension crénaux de valeurs extrème 0 et E. Quelle doit être la valeur de la période T du signal en crénaux pour que la charge et la décharge successives ne s'effectuent qu' à 63 % ? A B C D E F ( vrai) 30 ms 10 ms 5 ms 15 ms 25 ms autre Analyse : constante de temps du dipôle RC : t = RC = 500*20 10-6 = 10-2 s = 10 ms. La charge atteint 63 % de sa valeur au bout de 10 ms ; la décharge dure également 10 ms. période du signal crénaux : 10 + 10 = 20 ms.

retour -menu