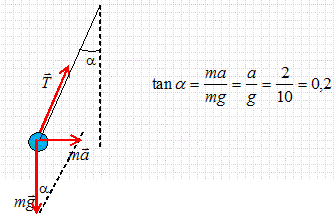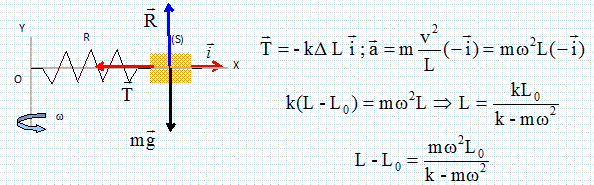QCM chute, oscillateur, accélération, travail, solide sur une glissière circulaire( Kiné EFOM 2009)

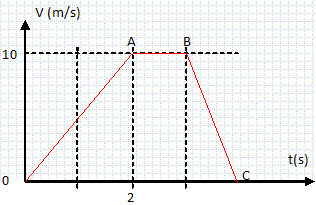
Le diagramme temporel de la vitesse d'un point décrivant une trajectoire rectiligne ( suivant Ox) est donné ci-dessous : accélération. Déterminer l'accélération aOA de l'étape OA et l'accélération aBC de l'étape BC. A( vrai) B C D ( vrai) E F aOA = 5 m s-2. aOA = 7,5 m s-2. aBC = 5 m s-2. aBC = -10 m s-2. aBC = -7,5 m s-2. autres Analyse : aOA = coefficient directeur du segment de droite OA : 10/2 = 5 m s-2. aBC = coefficient directeur du segment de droite BC : -10/1 = -10 m s-2. distance parcourue. Déterminer la distance parcourue par le mobile durant les 2 premières secondes. A B( vrai) C D E F x2 =7,5 m x2 =10 m x2 =15 m x2 = 20 m x2 =25 m autres Analyse : La vitesse est une primitive de l'accélération v = aOA t + v0 avec v0 = 0 ; v = 5 t. La distance est une primitive de la vitesse : x = ½aOA t2+x0 avec x0 = 0 ; x = 2,5 t2. remplacer t par 2 : x2 = 2,5*4 = 10 m. distance parcourue. Déterminer la distance parcourue par le mobile durant les 4 premières secondes. A B C ( vrai) D E F x4 =15 m x4 =20 m x4 =25 m x4 =30 m x4 =35 m autres Analyse : La distance AB est parcourue à vitesse constante v = 10 m/s ; la durée du parcours est t = 1s ; la distance parcourue est 10 m. Parcours BC : v = aBC (t -3)+ 10. x = ½aBC (t -3)2+ 10(t -3) + 20 remplacer t par 4 : x = -5+10+20 =25 m. 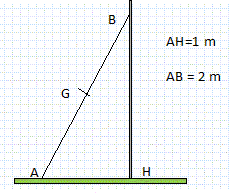Travail du poids. La poutre AB, de masse m = 20 kg est posée sur le sol. On la soulève pour la mettre contre le mur. g = 10 m s-2 ; 3½ =1,7. Quel est le travail effectué par le poids de la poutre au cours de l'opération ? A B C D E F ( vrai) 566 J -566 J -600 J +600 J -400 J autres Analyse : L'angle A vaut 60 ° ; BH = AB sin 60 = 2*0,866 = 1,7 m Le centre de gravité de la poutre passe de l'altitude 0 à l'altitude h = 0,85 m. Le travail du poids est résistant ( négatif) en montée. W = -mgh = -20*10*0,85 = -170 J. 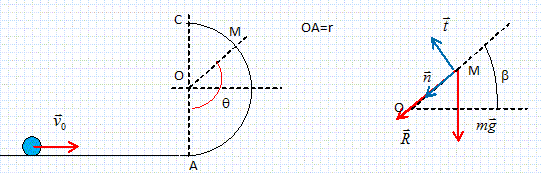solide sur une glissière circulaire Un solide ponctuel de masse m est lancé sur une glissière circulaire. Les frottements sont négligés.   Analyse : A- la norme de R est R =mv02/r + mg(3cosq-2) . Vrai. Projection des forces suivant MO : R +mg sin ß = m v2/r avec sin ß =sin (q-90) = - cos q. R =mg cos q +m v2/r Théorème de l'énergie cinétique entre A et M : ½mv2-½mv02 = - mg(r +r sin ß) = -mgr(1-cos q) v2/r = v02/r -2g(1-cos q). Le travail du poids est résistant en montée ; R perpendiculaire à la vitesse ne travaille pas. d'où R =mg cos q +m v02 /r - 2mg(1-cos q) R = m v02 /r +3mgcos q -2mg. B- la norme de R est R =mv02/r - mg(3cosq-2) . Faux. L'équilibre n'est pas déplacé, il est atteint plus rapidement. C- la valeur minimale de v0 pour que le mobile atteigne le sommet C est : v0 = (5gr)½. Vrai. En C la vitesse n'est pas nulle, mais R doit être positive ou nulle, sinon c'est la chute avant d'arriver en C. R = m v02 /r +3mgcos q -2mg =0 avec cos q = cos180 = -1 v02 /r = 5g ; v0 = (5gr)½. D- la vitesse minimale du mobile en C est : v2 = 2gr. Faux. v2 = v02 -2gr(1-cos 180) = v02 -4gr. E- la vitesse du mobile en C est : v2 = gr. Vrai. pendule dans un véhicule. un véhicule est animé d'un mouvement de translation rectiligne horizontal d'acélération a constante ( a = 2 m s-2) relativement à un repère galiléen. On suspend au plafond du véhicule unpendule constitué d'un fil de longueur L et d'une petite bille de masse m. On appelle a l'angle que fait le fil avec la verticale. La valeur de cet angle est donne par la relation suivante : A B C( vrai) D E F sin a = 1/5 cosa = 2/3 tan a = 0,2 sin a = 1/3 sin a = 0,5 autres Analyse :     chute libre. Un corps de masse m = 20 kg tombant en chute libre sans vitesse initiale, arrive sur le sol à la vitesse de 72 km/h . on prend g = 10 m s-2. Calculer la hauteur de la chute. A B ( vrai) C D E F 54 m 20 m 15 m 36 m 11 m autres Analyse : Théorème de l'énergie cinétique entre l'instant de départ et l'arrivée au sol. Le travail du poids est moteur en descente : W = mgh ½mv2 -0 = mgh ; h = v2 / (2g) avec v = 72 / 3,6 = 20 m/s. h = 20*20 / 20 = 20 m. Calculer la durée de la chute. A B C D ( vrai) E F 0,9 s 1,5 s 2,7 s 2 s 1,2 s autres Analyse Axe vertical descendant, origine au point de départ : z = ½gt2 : t = (2z/g)½ = (2*20/10)½ = 2 s Calculer le travail du poids au cours de la chute. A B C D E( vrai) F 150 J 900 J 1600 J 2800 J 4000 J autres Analyse : Travail moteur du poids en descente : w=mgh = 20*10*20 = 4000 J. Calculer l'énergie cinétique finale du corps. A B C D E( vrai) F 150 J 900 J 1600 J 2800 J 4000 J autres Analyse : ½mv2 = 0,5*10*202 = 4000 J rotation. La tige tourne à vitese angulaire constante w autour de D. Le solide a une masse m ; les frottements sont négligés. On note k la raideur du ressort. Le solide se stabilise et le ressort est alors allongé de D L. On note L0 la longueur à vide du ressort. Expression de D L . A( vrai) B C D E F m L0w2/ (k-mw2) m L0w2/ (k+mw2) (k-L0w2)/(mw2) L0w2/ (k+mw2) m L0w / (kw-m) autres Analyse :

retour -menu