Looping, génératrice et moteur, choc ( Kiné EFOM 2001)

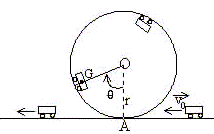
On considère un dispositif (dénommé "looping") constitué de deux rails d'abord horizontaux puis enroulés suivant une circonférence verticale de centre O et de rayon r, et, enfin, de nouveau horizontaux.Un véhicule de petites dimensions, assimilable à son centre d'inertie G, arrive en A avec la vitesse v0. On néglige tous les frottements. Soit G un point de la trajectoire dont la position est définie par (OA,OG) = q. On supposera OG = r2. Exprimer la vitesse v du véhicule au point G en fonction de g, r2, v0 et q. L'action du rail, perpendiculaire à la vitesse, ne travaille pas ; le travail du poids est résistant en montée. La différence d'altitude entre G et A vaut h = r2(1-cos q ) ; travail du poids : W= -mgh = -mg r2(1-cos q ) variation de l'énergie cinétique : DEc = ½mv2G-½mv2A. théorème de l'énergie cinétique : ½mv2G -½mv20 = -mg r2(1-cos q ) ; v2G = v20 -2g r2(1-cos q ). vG = [ v20 -2g r2(1-cos q )]½.   Soit R la réaction des rails sur le véhicule. Etablir l'expression de la réaction R au point G en fonction de m, g, r2, v0 et q. En déduire la valeur minimale de R. Puis remplacer v2M = v20 -2g r2(1-cos q ). R = m(g cos q+ v20/r2 -2g (1-cos q )) ; R = m(3gcos q -2g+ v20/r2). Pour une vitesse v0 donnée, R est minimale si cos q =-1. Rmini = m(-5g + v20/r2 ). Déterminer la valeur minimale de v0 pour que le véhicule décrive un tour complet à l'intérieur du looping, en restant constamment en contact avec les rails. Données : g = 10 m.s-2 ; r2= 10 cm ; 5½=2,24. La valeur minimale de R est nulle pour q =180° ( point le plus haut). soit v02 = gr2 ; v0 = (5gr2)½ = (0,1*5*10) =2,24 m s-1. Quelle est alors la vitesse du véhicule à son deuxième passage au niveau du point A ? Entre le premier passage en A et le second passage en A, aucune force de travaille. ( le poids ne travaille pas car l'altitude de départ et celle d'arrivée sont les mêmes). Le théorème de l'énergie cinétique indique que la valeur de la vitesse en A est v0.   Une génératrice G de f.é.m. E = 62 V et de résistance interne r = 2 ohm, alimente un moteur électrique M, de f.c.é.m. E' = 48 V et de résistance interne r' = 2 0 ohm. La ligne est composée de deux fils de cuivre PA et NB. Chacun de ces fils possède une résistance R = 5 ohm. Déterminer l'intensité I du courant débité par la génératrice. 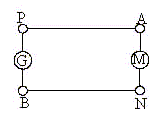Additivité des tensions : UBP = UB N + UNA + UAP E-r I = RI + E'+r'I + RI I = (E-E') / (2R+r+r') = (62-48) / ( 10+2+2) = 14/14 = 1,0 A. Déterminer les tensions U et U' aux bornes du générateur et du moteur. En déduire la chute de tension le long de cette ligne: U - U'. U = E-rI = 62-2*1 = 60 V ; U' = E'+r'I = 48+2*1 = 50 V ; U-U' = 10 V. Le courant passe pendant un intervalle de temps Dt = 100 s. Déterminer : - l'énergie électrique Wél fournie par la génératrice au reste du circuit : Wél = UIDt = 60*1*100 = 6,0 kJ. - l'énergie électrique W'él reçue par le moteur de la part du reste du circuit : W'él = U'IDt = 50*1*100 = 5,0 kJ. - la chaleur dégagée par la ligne, qui est en régime permanent : 2RI2 Dt = 10*12*100 = 1 kJ. - le rendement h de la ligne. Le rendement dépend-il de la durée du passage du courant ? Données : 4,8/6,2 = 0,774 ; 5/6 = 0,833 h = énergie reçue par le moteur / énergie fournie par le générateur = UE' IDt / (U IDt) = U'/U = 50/60 = 0,833 ~ 0,83. La génératrice est actionnée par une turbine, le moteur fait tourner l'arbre d'une machine-outil. Déterminer le travail fourni par la turbine à la génératrice, pendant 100 s. EIDt = 62*1*100 = 6,2 kJ. Déterminer le travail fourni par le moteur à la machine-outil, pendant 100 s. E'IDt = 48*1*100 =4,8 kJ. Les appareils sont en régime permanent, l'effet Joule représente pratiquement la seule source de chaleur. Définir et déterminer le rendement de l'installation: génératrice, ligne, moteur. h = énergie mécanique utile / travail fourni par la turbine = E' IDt / (E IDt) = E'/E = 48/62 = 0,774 ~ 0,77. Un solide S1, de masse ml, est lâché sans vitesse initiale d'un point A et glisse sur un plan incliné d'un angle alpha sur l'horizontale. Après un parcours AB, il aborde un plan horizontal sur lequel il continue à glisser avant de heurter un solide S2 de masse m2, immobile avant le choc. Les frottements sont négligeables. 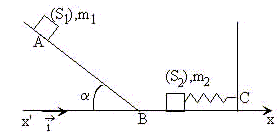Donnée s: ml = 50 g ; m2 = 200 g ; AB = 1 m ; sin (alpha) = 0,45 ; cos (alpha) = 0,89 ; tan (alpha) = 0,50 ; k = 25 N.m-1 . Déterminer la norme v1 de la vitesse de S1 juste avant le choc avec S2. L'action du plan, perpendiculaire à la vitesse, ne travaille pas ; le travail du poids est moteur en descente. La différence d'altitude entre B et A vaut AB sin a ; travail du poids : W= mgAB sin a variation de l'énergie cinétique : DEc = ½mv2B-0. théorème de l'énergie cinétique : ½mv2B = mgAB sin a ; v2B = 2gAB sin a ; Sur le plan horizontale le poids et l'action du plan, perpendiculaires à la vitesse, ne travaillent pas : la vitesse ne varie donc pas. v2B = v21 ; v1 = [ 2gAB sin a ]½.   v1 = (2*10*1 *0,45)½ =3,0 m/s.   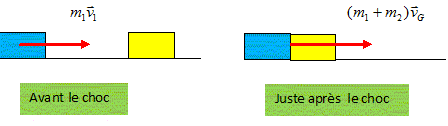Au moment du choc, il y a accrochage des deux solides qui forment alors un ensemble S de centre d'inertie G. En appliquant le principe de conservation du vecteur quantité de mouvement au système (S1, S2), calculer la norme vG de la vitesse de G juste après le choc. Conservation du vecteur quantité de mouvement : vG = m1 v1/(m1+m2) = 50*3 / (250) = 3/5 = 0,60 m/s. Le solide S2 est relié à un ressort de masse négligeable, à spires non jointives, de constante de raideur k et dont l'autre extrémité C est fixe. Juste avant le choc, ce ressort est au repos. Après le choc, l'ensemble S reste lié au ressort et il continue son mouvement, les spires du ressort étant encore non jointives. La position de G sera repérée sur l'axe x'x indiqué sur la figure, avec pour origine la position de G à l'instant du choc. On prendra pour origine des temps l'instant du choc. Etablir l'équation différentielle de l'oscillateur constitué par le ressort et les deux masses accolées. Ecrire la seconde loi de newton sur un axe horizontal orienté vers la droite : -kx = (m1+m2) x" ; x" + k/(m1+m2) x=0. On pose w2= k/(m1+m2) = 25 / 0,25) =100 ; w = 10 rad/s. En déduire l'équation horaire x(t) du mouvement. x(t) = Asin (wt + f ) x(0) = 0 = A sinf ; f = 0 ou pi radian. vitesse : x'(t) = Aw cos (wt + f ) x'(0) =v1 = Aw cos f d'où f = 0 A = v1/w = 0,6 / 10 = 0,06 m = 6 cm. x(t) = 0,06 sin (10t ).

retour -menu