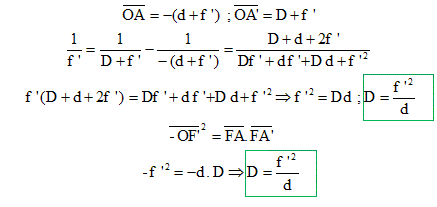Lentilles minces, Descartes, Newton, constructions concours kiné Ceerrf 2009.

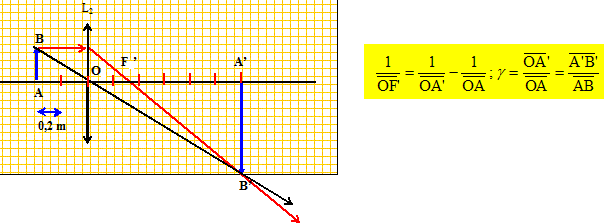
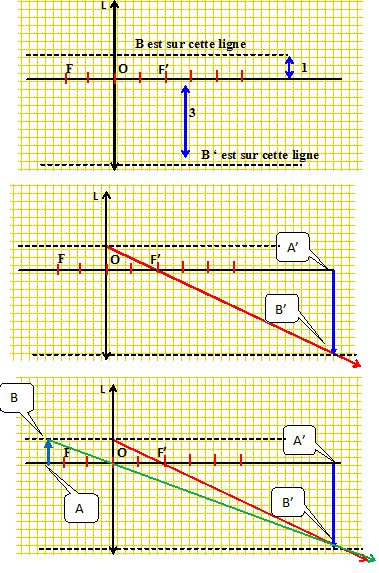
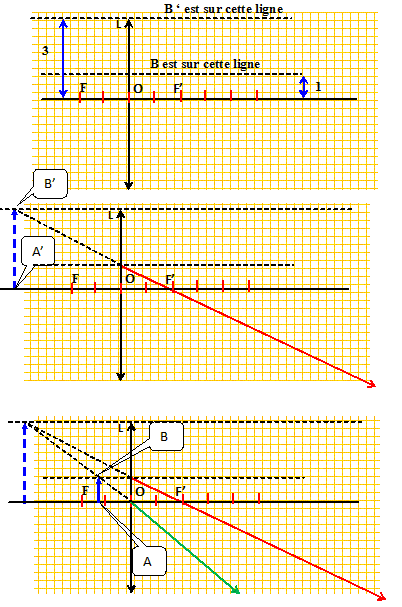
On considère une lentille mince convergente (L) de centre optique O et de distance focale image f', un objet étendu AB et A'B' l'image de cet objet au travers de la lentille.  Rappeler les formules de conjugaison et du grandissement pour une lentille mince. Sont-elles applicables pout tout type de lentilles minces ? Ces formules s'appliquent aux lentilles minces convergente et divergente.  Expliquer de façon succinte ( 2 lignes maximum) pourquoi :. A'B' est à l'infini si AB est dans le plan objet. On écrit les distances algébriques en gras et en bleu. 1/OA' tend ves zéro donc 1/OA = -1/OF' = 1/ OF A'B' est dans le plan focale image si AB est à l'infini. 1/OA tend ves zéro donc 1/OA' =1/OF' .   Si AB est devant la lentille et A'B' après la lentille, l'image est inversée. OA <0 ; OA' >0 ; g = OA' / OA est négatif ; à un grandissement négatif, correspond une image inversée par rapport à l'objet. Si AB et A'B' sont avant la lentille, alors l'image est droite.  OA <0 ; OA' <0 ; g = OA' / OA est positif ; à un grandissement positif, correspond une image droite par rapport à l'objet.. Il existe une autre formule de conjugaison si on utilise les foyers objet et image F et F' d'une lentille mince comme origine au lieu du centre optique O. En effectuant ce changement d'origine, établir la relation entre FA, F'A' et f' ( formule de Newton). On considère une lentille mince telle que f' = 3,0 cm, un objet AB situé à gauche du foyer F ( à une distance d de celui-ci), une image A'B' située à droite du foyer image ( à une distance D de celui-ci) Exprimer D à partir des formules de Descartes. Dans ce cas de figure la formule de Newton n'est pas plus adaptée ? Justifier. On donne d = 5,0 cm, calculer D( en m) D = (0,03)2 / 0,05 =1,8 10-2 m. Exprimer puis calculer le grandissement : g =(D+f ' ) / (-(d+f ')) = -(D+f ' ) / (d+f ') = -(1,8 +3) / (5+3) = -0,6. Caractériser l'image A'B'. image réelle, plus petite que l'objet et de sens contraire par rapport à l'objet.   On considère la lentille précédente. Déterminer par construction la position d'un objet AB et d'une image A'B' vérifiant g = -3.   Déterminer par construction la position d'un objet AB et d'une image A'B' vérifiant g = +3.

c

retour -menu