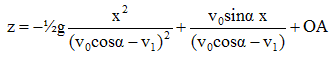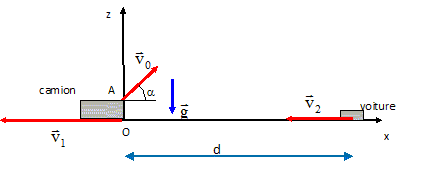
Projection d'un caillou d'un camion en mouvement concours kiné Ceerrf 2009.

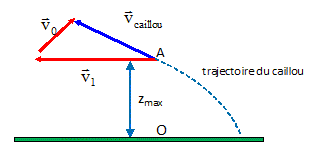
Un caillou assimilé à son centre d'inertie G est projeté à l'arrière d'un camion dans le plan vertical. A l'instant t=0 le caillou est en A, a une vitesse v0 dans le référentiel terrestre, qui fait un angle a = 45 ° avec l'horizontale. Les frottements sont négligés. Le camion roule à une vitesse constante v1. Etablir littéralement les équations horaires du caillou dans le repère orthonormé.  Le caillou n'est soumis qu'à son poids ; la seconde loi de Newton conduit à l'accélération dont les composantes sont : (0 ; -g ) Hypothèse 1 : le caillou est projeté à partir du camion en mouvement. Vecteur vitesse du caillou à t=0 dans le repère (x O z) : Composantes du vecteur vitesse initiale : ( v0 cos a -v1 ; v0 sin a ) ; position initiale ( 0 ; OA) La vitesse est une primitive de l'accélération : ( v0 cos a -v1 ; -gt + v0 sin a ) La position est une primitive du vecteur vitesse : x= (v0 cos a -v1 ) t (1) ; z = -½gt2 +v0 sin a t + OA.(2) Etablir l'équation cartésienne z=f(x). (1) donne t = x /(v0 cos a -v1 ) ; repport dans (2). Hypothèse 2 : il faut imaginer le caillou est en A, projeté par le camion ( le caillou n'est pas sur le camion). Dans les expressions précédentes, supprimer v1. Ecrire littérallement, en justifiant, sans calculs compliqués, l'équation horaire du caillou dans le référentiel du camion, auquel on associe un repère orthonormé (x' Oz') qui coïncide avec le repère ( x O z) à t=0. Hypothèse 1 : le caillou est projeté à partir du camion en mouvement. Le caillou est initialement immobile sur le camion. Dans les expressions ci-dessus remplacer (v0 cos a -v1 ) par : v0 cos a x' = (v0 cos a) t ; z' = -½gt2 +v0 sin a t+ OA. Hypothèse 2 : il faut imaginer le caillou est en A, projeté par le camion ( le caillou n'est pas sur le camion). Dans l'expression précédente, remplacer (v0 cos a) par (v0 cos a+ v1). A t=0, une voiture distante de d, suit le camion, selon la direction Ox, avec une vitesse constante v2. Ecrire l'équation horaire x1(t) du mouvement de la voiture dans le repère (x O z) : x1(t) = -v2 t + d. Ecrire l'équation horaire x'1(t) du mouvement de la voiture dans le repère (x' O z'). x'1(t) = (v1-v2) t + d. Etablir littéralement la condition nécessaire pour que le caillou retombe sur la route avant le passage de la voiture. On note tS l'instant où le caillou atteint le sol. Dans le référentiel lié au sol ( x O z ) : l'abscisse du point de chute x(tS) doit être inférieure à l'abscisse de la voiture x1(tS). x= (v0 cos a -v1 ) tS ; x1(t) = -v2 tS + d. (v0 cos a -v1 ) tS <-v2 tS + d. Calculer tS. v0 = 10 m/s ; OM = 1,6 m ; v1 = 30 m/s ; v2 = 20 m/s ; g = 10 m s-2 ; 27*16 = 432 ; sin 45 = 0,7.   z = -½gtS2 +v0 sin a tS + OA = 0 -5 tS2 +10*0,7 tS + 1,6 = 0 ; tS2 -1,4 tS -0,32 = 0 D = 1,42+4*0,32 = 3,24 ; D½ =1,8 ; tS= (1,4+1,8) / 2 = 1,6 s.   En déduire les valeurs possibles pour d, permettant d'éviter la chute sur la voiture. La voiture a une hauteur H supérieure à la côte maximale zM atteinte par le caillou au cours de son mouvement. Hypothèse 1 : le caillou est projeté à partir du camion en mouvement.   Abscisse du caillou lorsque celui-ci est au sol : x= (v0 cos a -v1 ) tS = (7-30)*1,6 = -36,8 m. Abscisse de la voiture à cette même date : x1(t) = -v2 tS + d = -20*1,6 + d = -32+d. Le caillou tombe sur la voiture si : -32+d < -36,8 d <-4,8 m. Une distance ne peut pas être négative : le caillou ne tombe pas sur la voiture, le camion va trop vite par rapport à la voiture. Hypothèse 2 : il faut imaginer le caillou est en A, projeté par le camion ( le caillou n'est pas sur le camion). Abscisse du caillou lorsque celui-ci est au sol : x= (v0 cos a ) tS = 7*1,6 = 11,2 m. Abscisse de la voiture à cette même date : x1(t) = -v2 tS + d = -20*1,6 + d = -32+d. Le caillou ne tombe pas sur la voiture si : -32+d > 11,2 d >43,2 m.

c

retour -menu