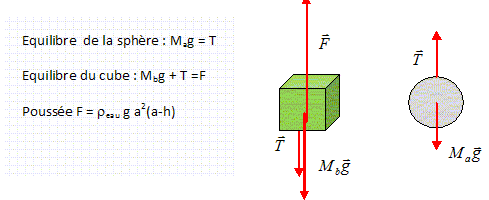QCM mécanique : Archimède, pendule, Kepler, moteur électrique( Kiné Berck 2009)

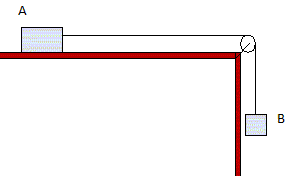
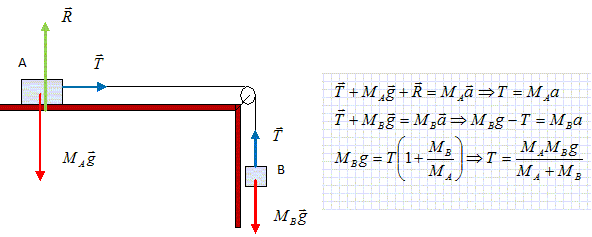
Un solide de masse MA est posé sur une table horizontale. Il est relié par l'intermédiaire d'un fil inextensible et de masse négligeable à un solide B de masse MB. Le solide B lâché sans vitesse initiale entraîne le solide A. On suppose que le fil reste toujours tendu et que tous les frottements sont négligeables. On admettra que la tenion du fil a même valeur sur chaque brin de part et d'autre de la poulie. MA = 8,0 kg ; MB = 3,5 kg ; g = 9,81 m s-2. Déterminer la valeur de la tension du fil ( en N). A B ( vrai) C D E F 4,0 24 27 32 61 aucune réponse exacte Analyse : T = 8*3,5*9,81 / (8+3,5) =23,9 N ~ 24 N. Un cube de bois de côté a = 8,0 cm est relié à une sphère de rayon r = 1,0 cm par un fil inextensible de masse négligeable. Le système est plongé dans l'eau de mer. A l'équilibre le cube émerge d'une hauteur h. On ne tient pas compte de l'action de l'air sur la partie émergée du cube. 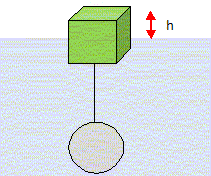On donne rbois = 7,40 102 kg m-3 ; racier = 7,80 103 kg m-3 ; reau mer = 1,03 103 kg m-3 ; Déterminer la hauteur h ( en cm). A B C( vrai) D E F 1,2 1,5 1,8 2,1 2,3 autre Analyse : Ma = 4/3 pi r3 racier =4/3 *3,14 * (10-2)3 * 7,80 103 =3,266 10-2 kg Mb =a3 rbois = 0,083 *740 =0,3789 kg. 0,379 *9,81 + 3,27 10-2 *9,81 = 1,03 103 *9,81 *0,082(0,08-h). 0,3789 +3,266 10-2 =6,592 (0,08-h) ; 0,08-h = 0,0624 ; h = 0,01752 m ; h = 1,8 cm. pendule On considère une table inclinée d'un angle a sur l'horizontale. Un petit mobile autoporteur de masse m = 135 g est suspendu à u point fixe M par un fil inextensible de masse négligeable dont la longuer est L = 38,2 cm. On néglige les frottements. La période des oscillations de faible amplitude de ce pendule est : T = 2 pi [L / (g sin a )]½. On veut que la période T de ce pendule soit égale à la période des oscillations non amorties et de faible amplitude d'un pendule simple de même longueur L qui oscillerait à la surface de Mars. Masse de Mars M = 6,42 1023 kg ; rayon de Mars : R = 3,4 103 km ; G = 6,67 10-11 SI. Calculer a en degré. A( vrai) B C D E F 22 27 32 36 38 autre Analyse : T = 2 pi [L / (gterre sin a )]½ =2 pi [L / gmars ]½ ; d'où : gterre sin a = gmars. gmars= GM / R2 = 6,67 10-11 * 6,42 1023 / (3,4 106)2=3,704 m s-2. sin a = gmars/ gterre = 3,704/9,81 =0,3776 ; a =22°. On considère que les orbites de Vénus et de la Terre sont des cercles dans le référentiel héliocentrique. La période de révolution de Vénus est de 224,7 jours. Le rayon de l'orbite de la terre est 1,50 108 km, ce qui correspond à 1 U.A. Calculer le rayon de l'orbite de Vénus ( en U.A). A B C D E( vrai) F 0,46 0,52 0,61 0,66 0,72 autre Analyse : 3ème loi de Kepler : T2Vénus = k R3Vénus avec k une constante T2Terre = k R3Terre avec R = 1 U.A ; T2Terre = k T2Vénus = T2Terre R3Vénus ; R3Vénus = T2Vénus / T2Terre = (224,7 / 365,25)2 =0,3784 RVénus =0,37841/3 =0,72.     Moteur électrique. Un moteur est branché à une pile de fem E = 6,0 V et de résistance interne r = 1,2 ohms. Le générateur fourni une puissance électrique de 2,8 W au moteur qui en convertit 80 % en énergie mécanique. Déterminer la résistance électrique ( ohms) du moteur. A ( vrai) B C D E F 2,1 4,2 6,7 8,2 9,8 autre Analyse : Puissance électrique fournie au moteur : 2,8 = U I avec U = E-rI = E'+r'I ( E' : fcem du moteur) 2,8 = (E-rI) i = (6,0-1,2 I) I 2,8 = 6,0 I -1,2 I2 ; I2-5 I +2,33 = 0; résoudre I = 0,52 A. Puissance mécanique : E'I ; puissance Joule : r'I2. E'I = 0,8*2,8 = 2,24 W ; E' =  2,24/0,52 = 4,3 V r'I2 = 0,2*2,8 =0,56 W r' = 0,56/0,522 =2,1 ohms.

retour -menu