Titrage par conductimétrie de l'ion magnésium concours kiné Assas 2009.

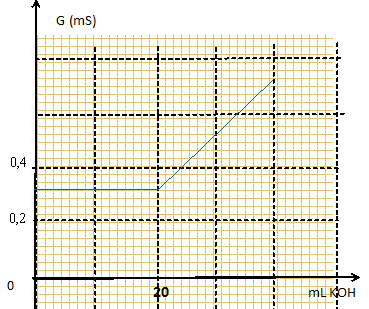
On souhaite titrer les ions magnésium présents dans une solution S0 de chlorure de magnésium. Le volume de la solution est V = 100 mL. On dispose d'une cellule de conductimétrie dont les électrodes, distantes de 4,00 cm, ont chacune une surface de 5,00 cm2. Le titrage s'effectue par ajout d'une solution d'hydroxyde de potassium de concentration en soluté apporté égale à 1,00 10-2 mol/L. Cet ajout entraîne la précipitation de l'hydroxyde de magnésium. Le graphe ci dessous représente la variation de la conductance G( mS) du mélange réactionnel en fonction du volume V( mL) d'hydroxyde de potassium ajouté. Avant l'équivalence, l'ion Mg2+ est en excès : du point de vue de la conductimétrie, tout se passe comme si on remplaçait l'ion magnésium par deux ions potassium. Mg2+aq + 2K+aq +2 HO- aq = Mg(OH)2 (s) + 2K+aq Or lMg2+ = 10,5 10-3 S m2 mol-1 et lK+ =7,40 10-3 S m2 mol-1 . La conductivité de la solution ( donc la conductance) reste à peu près constante. Après l'équivalence, l'ion hydroxyde est en excès : on ajoute à la solution des ions hydroxyde et potassium. Or lHO- = 19,8 10-3 S m2 mol-1 est assez grande. La conductivité( donc la conductance) de la solution va croître assez rapidement. L'intersection des deux segments donne le volume équivalent VE = 20,0 mL. Concentration des ions Mg2+ dans la solution : Mg2+aq +2 HO- aq = Mg(OH)2 (s) A l'équivalence : quantité de matière d'ion hydroxyde : 20,0 10-3 * 1,00 10-2 = 2,00 10-4 mol. D'après les nombrs stoechiométriques de l'équation support du dosage : n(Mg2+ ) = ½n(HO- )= 1,00 10-4 mol dans 0,1 L de solution [Mg2+] = 1,00 10-4 /0,1 = 1,00 10-3 mol/L.   Le pH de la solution S0 est voisin de 7,0. Calculer la conductivité et la conductance de la solution S0. Ions présents dans la solution initiale : HO-aq, H3O+aq, Mg2+aq et Cl- aq. Concentration : [HO-aq] = [H3O+aq] = 1,0 10-7 mol /L = 1,0 10-4 mol m-3. [Mg2+aq] =1,0 mol m-3 ; [Cl- aq] = 2 [Mg2+aq] =2,0 mol m-3. lMg2+ = 10,5 10-3 S m2 mol-1 ; lHO- =19,8 10-3 S m2 mol-1 ; lH3O+ = 35,0 10-3 S m2 mol-1 ; lCl- =7,60 10-3 S m2 mol-1 . Conductivité s = lMg2+[Mg2+aq] + lCl- [Cl- aq] + lHO- [HO-aq] + lH3O+[H3O+aq] s = 10-3 [10,5 + 7,6*2 +19,8* 10-4 +35 *10-4 ] = 2,57 10-2 S m-1. Constante de cellule : k = S/e = 5,00 10-4 / 4,00 10-2 =0,0125 m Conductance G = k s =0,0125*2,57 10-2 = 3,21 10-4 S = 0,321 mS = 321 µS.   La tension aux bornes du circuit électrique de mesure de la conductance est 0,500 V. Calculer l'intensité du courant qui traverse le circuit. Résistance électrique du circuit R = 1/G = 1/3,21 10-4 =3,115 103 ohms. I= U/R = 0,500 / 3,115 103 =1,61 10-4 A. La constante d'équilibre de précipitation de l'hydroxyde de magnésium a pour valeur K= 5,00 10-10. Calculer les concentrations molaires volumiques des ions magnésium et hydroxyde au point équivalent. Mg(OH)2 (s) = Mg2+aq +2 HO- aq K =[Mg2+]éq [HO-]2éq avec [HO-]éq = 2 [Mg2+]éq K = 4 [Mg2+]3éq = 5,00 10-10 ; [Mg2+]éq =5,00 10-4 mol/L = 0,500 mol m-3 ; [HO-]éq = 1,00 mol m-3. Comparer la conductivité due a ces ions et celle due aux ions spectateurs. Conclure. lMg2+[Mg2+aq]éq + lHO- [HO-aq]éq = 10-3[10,5*0,5 +19,8]=2,51 10-2 S m-1. lCl-[Cl- aq] éq + lK+ [K+aq]éq ; il faut tenir compte du facteur de dilution (100+20) / 100 = 1,2. [Cl- aq] éq = 2/1,2 =1,67 mol m-3 ; [K+aq]éq = 2 10-4 / 0,12 =1,67 10-3 mol/L = 1,67 mol m-3. lCl-[Cl- aq] éq + lK+ [K+aq]éq = 10-3[7,6 +7,4]*1,67=2,50 10-2 S m-1. Les deux valeurs des conductivités sont pratiquement identiques. Il va être difficile de déterminer avec précision le point équivalent. ( avec de telles concentrations, la réaction support du dosage conduit à un équilibre, elle n'est pas totale : elle ne peut pas servir à un dosage ).

c

retour -menu