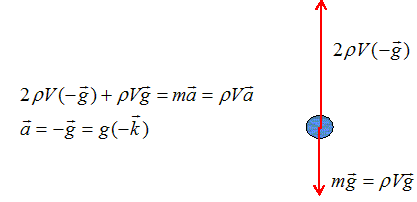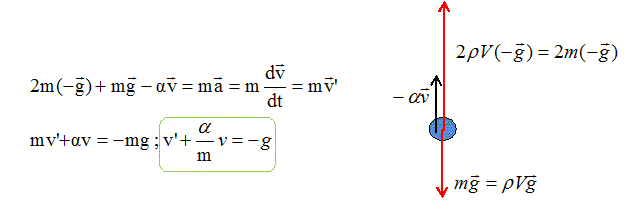Chute verticale d'une balle de bois dans l'eau concours kiné Assas 2009.

On lâche une balle de bois au dessus d'une surface d'eau. La balle est assimilée à son centre d'inertie G. A l'instant t=0 elle pénètre dans l'eau avec une vitesse v0 = 10 m/s. g = 10 m/s2 ; V : volume de la balle ; r : masse volumique de la balle ; r0 = 2r : masse volumique de l'eau. Mouvement dans l'eau : frottement négligé. Poussée d'archimède P et poids de la balle. poids de la balle : P= mg avec m = rV ; P =r g V ; poussée d'Archimède : P = r0 g V = 2r g V. La valeur de la poussée d'Archimède est égale à 2 fois la valeur du poids de la balle. Accélération, vitesse et position de G. Ecrire la seconde loi de Newton : La vitesse est une primitive de l'accélération : v = -gt + v0. La position est une primitive de la vitesse : z = -½gt2 +v0t. Profondeur maximale atteinte. La vitesse s'annule, puis la balle remonte. A cet instant t1 = v0 / g = 10 /10 = 1 s. Repport dans l'expression de z : zmax= -0,5*10 +10 = 5 m. Mouvement dans l'eau : frottement non négligé. A l'instant t=0 la balle pénètre dans l'eau avec une vitesse v0 = 10 m/s. La force de frottement est colinéaire à la vitesse et de sens contraire. Sa valeur est f = av avec a = 0,05 SI ; Masse de la balle m = 100 g. Equation différentielle vérifiée par la vitesse : La solution de cette équation est du type : v(t) = A + B exp(-t/t) avec t = m/a. ( A et B sont des constantes). Expression des constantes : v' = -B/t exp(-t/t) =-Ba/m exp(-t/t) ; repport dans l'équation différentielle : -Ba/m exp(-t/t) + a/mA + a/mBexp(-t/t) = -g ; a/mA =-g d'où A = -gm/a ; A = -gt. Au bout d'un temps très grand, la vitesse limite est atteinte : vlim = A = -gt A l'instant t=0, la vitesse vaut v0 ; v(t=0) = v0 = A + B ; B = v0 +gt = v0 +vlim. Cette vitesse s'annule t-elle ? Si oui à quelle date t2. 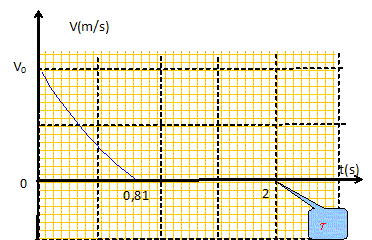L'accélération étant dirigée en sens contraire de l'axe, le mouvement est freiné : la vitesse va donc finir par s'annuler. v(t) = -gt + (v0 +gt) exp(-t/t) ; v(t2) = 0 = -gt + (v0+gt) exp(-t2/t). gt / (v0+gt) = exp(-t2/t) ; ln [gt / (v0 +gt)] = -t2/t ; t2 = t ln [v0 /(gt)+1]. t = m / a = 0,1/*0,05 = 2 s ; v0/(gt )=10 / (10*2) = 0,5 ; t2 = 2 ln 1,5 = 0,81 s. La vitesse limite ne sera pas atteinte lors de la descente. Courbe v= f(t).   La profondeur z(t) à laquelle se trouve la bille a pour expression : z(t) = K1 t + K2 exp(-t/t) +K3 où K1, K2, K3 sont des constantes. Par identification, et en utilisant la condition initiale, trouver les expressions littérales de ces constantes. z(0) = 0 d'où : 0 = K2 +K3 (1). La position est une primitive de la vitesse : v(t) = -gt + (v0 +gt) exp(-t/t) ; z(t) = -gt t - t (v0 +gt) exp(-t/t) + K3 On identifie K1 à -gt ; K1 = -10*2 = -20 m/s. K2 à - t (v0 +gt) ; K2 = -2( 10+20) = -60 m ; et K3 à t (v0 +gt) = 60 m z(t) = -20 t -60 exp(-t/t) +60 Profondeur maximale atteinte : zmax =-20 *0,81 -60 exp(-0,405) +60 = 3,8 m.

c

retour -menu